Gradient

Gradient

In 1-dim:
the derivative of function:
$\frac{df(x)}{dx}={\lim }_{x\to \infty }\frac{f(x+h)-f(x)}{h}$

In multiple-dim:
the gradient is a vector of (partial derivatives) along each dimension

Direction of gradient

Gradient의 방향 = 값이 가장 가파르게 증가하는 방향.
따라서 gradient-descent는 neg-gradient 방향으로 가야지.

Implementation

---

Numerical Calculation

optimization의 target인 $W$의 gradient를 직접 numerically 계산하는 것은 매우 힘들다.(gradient vector의 ndim 만큼 $d{W}_i$만큼씩 계산해야 하니, loop를 너무 많이 돌아야 함.)

• approximate
• slow
• easy to write

Numerical Differentiation

Newton’s difference quotient에 따르면,
$\frac{\partial f(x)}{\partial x}={\lim }_{h\to 0}\frac{f(x+h)-f(x)}{h}$
이지만, 아래처럼 대칭으로 계산하는게 더 낫다고 한다. Why??
$\frac{\partial f(x)}{\partial x}={\lim }_{h\to 0}\frac{f(x+h)-f(x-h)}{2h}$

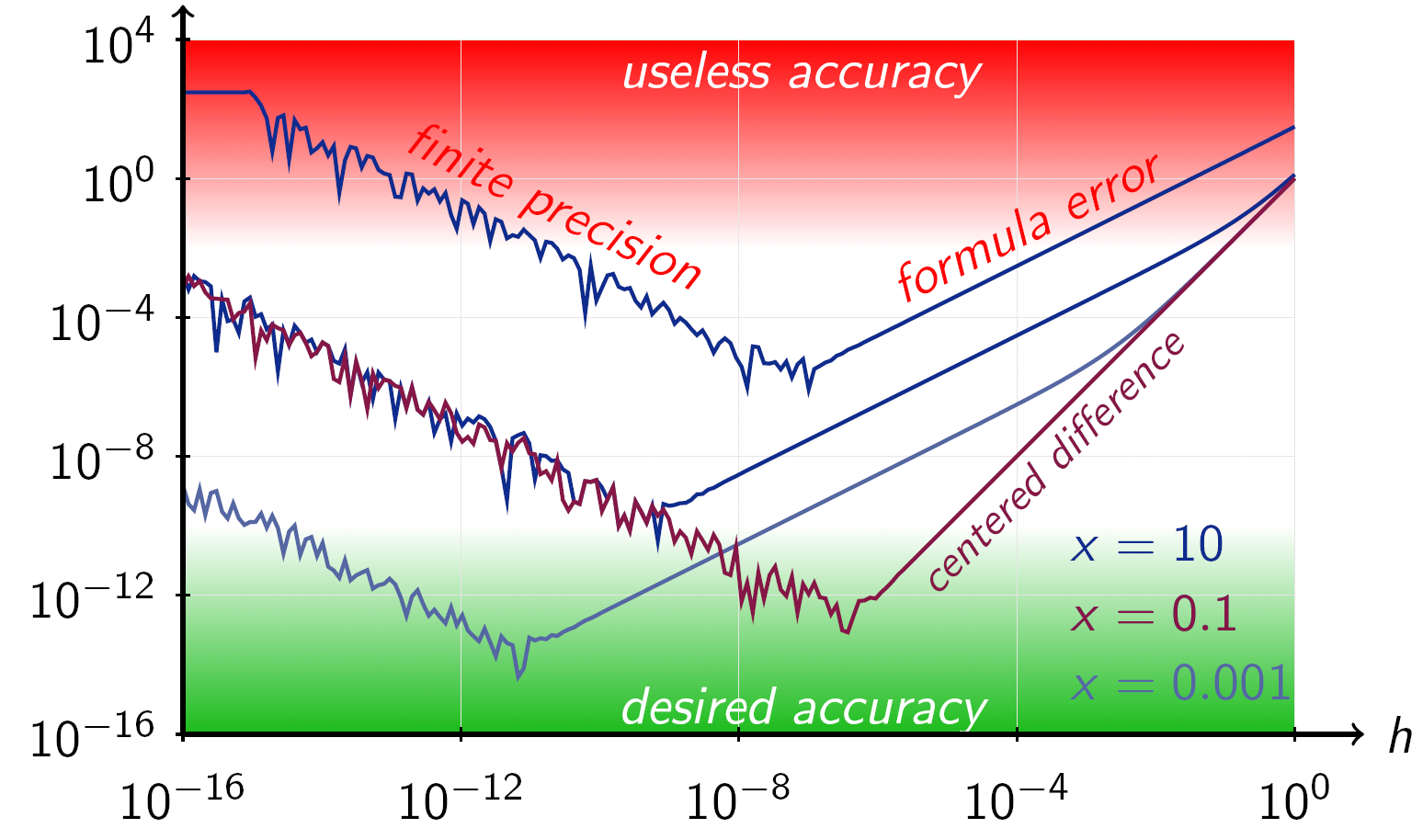
How to choose $h$?

For $h=0$ is undefined
Choose $h$ is trade-off:

• Rounding error(finite precision)
• Approximation error(wrong)

Elbow: $\sqrt[3]{ϵ}$ with $ϵ$ the machine precision
ex)

• $ϵ=6\times 10^{-8}$. for single precision(32 bits)
• $ϵ=1\times 10^{-16}$. for double precision(64 bits)

Analytic Calculation

$L=\frac{1}{L}{\sum }_{i=1}^N{L}_i+{\sum }_k{W}_k^2$
where

• Data loss: $\frac{1}{L}{\sum }_{i=1}^N{L}_i$,
• Regularization: ${\sum }_k{W}_k^2$
  라고 할 때, target은 ${\nabla }_{W}L$

tips!) Loss는 $W$의 함수이다.

it is,

• exact
• fast
• error-prone

Gradient check!

항상 gradient를 analytic하게 구할 줄 알아야 하지만, implementation을 numerical 하게 한다는 점을. 그리고 대응시켜본 다는 것을.