Overview

연구 배경: 인공지능 에이전트를 통해 의식 이론(HOT, GWT, IIT)을 구현하여 정보 접근, 통합, 모니터링 등의 기능적 측면을 검증하고자 함

핵심 방법론:

HOT, GWT, IIT 이론을 통합된 아키텍처에 구현하고 각 구성 요소를 체계적으로 손상시키며 인과적 필수성을 검증

적대적 잡음과 같은 시나리오를 적용하여 시스템의 견고성을 테스트

주요 기여:

첫 번째 차원 성능(작업 수행)과 두 번째 차원 인식(자기 인식)을 아키텍처 손상으로 분리하여 이론 검증

전역 브로드캐스트 기능이 잡음 증폭을 유발하는 현상(브로드캐스트-증폭 효과)을 실증

실험 결과:

실험 1에서 Type-2 AUROC 지표 0.78 달성, 실험 2에서 Global Broadcast Index(GBI) 0.89 기록

한계점: $Φ$ 값 직접 계산 대신 PCI-A 프록시를 사용하여 IIT 통합성 검증, 다국어 및 복잡한 환경에서의 일반성 미검증

Can We Test Consciousness Theories on AI? Ablations, Markers, and Robustness

Summary

이 섹션에서는 의식 이론이 AI에 적용될 수 있는지에 대한 탐구를 중심으로, Ablation 실험, 의식 마커(markers), 그리고 안정성(robustness)을 통한 평가 프레임워크를 제안한다. 핵심 접근법은 AI 모델의 특정 구성 요소를 제거하거나 조작하는 Ablation을 통해 의식과 관련된 행동 변화를 분석하는 것이며, 이를 통해 의식 마커(예: 자기 인식, 의도성)의 존재 여부를 검증한다. 또한, 다양한 조건 하에서 의식 마커의 일관성과 안정성을 평가함으로써, AI가 인간의 의식 특성과 유사한 패턴을 보이는지에 대한 실증적 근거를 모색한다. 이 연구는 기존의 의식 이론을 AI 시스템에 직접 적용하는 데 있어 체계적인 실험 설계와 평가 지표를 제공하며, 특히 의식 마커의 정의와 Ablation 실험의 설계 원칙을 명확히 정리한 것이 특징이다. 실험 결과는 특정 마커가 모델의 구조적 변화에 따라 유의미하게 변하는 것으로 나타나, AI의 의식 유무 판단에 있어 정량적 지표의 필요성을 강조한다.

Yin Jun Phua Institute of Science Tokyo phua@comp.isct.ac.jp

December 23, 2025

Abstract

The search for reliable indicators of consciousness has fragmented into competing theoretical camps (Global Workspace Theory (GWT), Integrated Information Theory (IIT), and Higher-Order Theories (HOT)), each proposing distinct neural signatures. We adopt a synthetic neuro-phenomenology approach: constructing artificial agents that embody these mechanisms to test their functional consequences through precise architectural ablations impossible in biological systems. Across three experiments, we report dissociations suggesting these theories describe complementary functional layers rather than competing accounts. In Experiment 1, a no-rewire Self-Model lesion abolishes metacognitive calibration while preserving first-order task performance, yielding a synthetic blindsight analogue consistent with HOT predictions. In Experiment 2, workspace capacity proves causally necessary for information access: a complete workspace lesion produces qualitative collapse in access-related markers, while partial reductions show graded degradation, consistent with GWT’s ignition framework. In Experiment 3, we uncover a broadcast-amplification effect: GWT-style broadcasting amplifies internal noise, creating extreme fragility. The B2 agent family is robust to the same latent perturbation; this robustness persists in a Self-Model-off / workspace-read control, cautioning against attributing the effect solely to zself compression. We also report an explicit negative result: raw perturbational complexity (PCI-A) decreases under the workspace bottleneck, cautioning against naive transfer of IIT-adjacent proxies to engineered agents. A simple composite of markers (GBI + ∆PCI + AUROC) predicts OOD fragility. These results suggest a hierarchical design principle: GWT provides broadcast capacity, while HOT provides quality control. We emphasize that our agents are not conscious; they are reference implementations for testing functional predictions of consciousness theories.

1 Introduction

Summary

이 섹션에서는 의식의 과학이 직면한 검증 위기를 지적하고, Global Workspace Theory (GWT), Integrated Information Theory (IIT), Higher-Order Theories (HOT) 등 주요 이론들의 생물학적 시스템에서의 검증 한계를 설명한다. 생물학적 뇌에서 정밀한 구조적 제거 실험이 어렵다는 점을 고려해, 합성 신경 현상학(synthetic neuro-phenomenology)을 제안한다. 이 접근법은 신경과학과 인공지능의 공통된 틈을 메우는 데 기여한다. 신경과학에서는 모든 뉴런과 활성화 상태를 관찰·조작 가능한 완벽한 모델 생물(perfect model organism)을 제공하고, 인공지능에서는 자체 모니터링(self-monitoring)과 강건성(robustness)을 높이는 데 이론적 기반을 제공한다. 기존의 시뮬레이션 시도는 이론적 메커니즘의 기능적 필수성(functional necessity)을 명확히 하지 못했으며, 단일 이론만을 적용하는 경향이 있었다. 본 연구는 강화학습 유형 아키텍처를 기반으로 한 에이전트를 설계하고, 정밀한 손상 실험(causal lesions), 노이즈 주입(noise titration), 적대적 보상 구조(adversarial reward structures) 등을 통해 이론의 기능적 효과를 검증한다. 결과적으로, 자체 모델(Self-Model) 제거 시 1차 작업 성능은 유지되나 메타인지 교정(metacognitive calibration)이 상실되는 합성 맹시(synthetic blindsight), 전송 용량 감소에 따른 접근 마커의 갑작스러운 붕괴(bus-off discontinuity), 전송 증폭 효과(broadcast-amplification)가 노이즈 감소 효과보다 우세한 점, IIT 관련 복잡성 지표(PCI-A)의 역전 등의 결과를 도출한다. 특히, B2 에이전트(B2 agent)는 기존 정규화 기법 하에서도 L75 > 0.50의 강건성을 유지하며, 노이즈 감소(noise-attenuation)를 아키텍처의 내재적 특성으로 인식한다. 이러한 결과는 이론적 메커니즘의 기능적 계층 구조(functional hierarchy)와 기술적 이론의 제약(transfer constraint)를 명확히 하며, 인공지능 시스템 설계에 새로운 통찰을 제공한다.

The science of consciousness faces a validation crisis. While theories like Global Workspace Theory (GWT) [Baars, 1988, Dehaene and Changeux, 2011], Integrated Information Theory (IIT) [Tononi, 2004, Oizumi et al., 2014], and Higher-Order Theories (HOT) [Rosenthal, 2005, Lau and Rosenthal, 2011] propose distinct neural signatures of awareness (ranging from non-linear “ignition” [Dehaene, 2014] and causal integration (Φ) [Oizumi et al., 2014] to metacognitive self-monitoring [Fleming et al., 2010]), testing them in biological systems is constrained by the inability to perform precise architectural ablations. We propose synthetic neuro-phenomenology: building agents that explicitly embody these theoretical commitments to test their functional utility.

This approach addresses a gap in both neuroscience and artificial intelligence. For neuroscience, synthetic agents offer a “perfect model organism” where every neuron, weight, and activation is observable and manipulable, allowing for causal tests that are ethically or technically impossible in biological brains. For AI, consciousness theories offer a potential roadmap for overcoming the brittleness of current systems [Bengio, 2017]. While deep learning has achieved broad success, modern models often lack the robustness, adaptability, and self-monitoring capabilities characteristic of biological intelligence. By implementing architectural priors derived from consciousness science (such as global broadcasting [Goyal et al., 2022] and self-modeling), we aim to determine whether these mechanisms confer the same functional advantages to artificial agents that they are hypothesized to provide to biological organisms.

However, prior attempts to model consciousness in silico have often fallen short of systematic validation. Many implementations rely on loose metaphorical translations of neural theories, where a simple feedback

loop is labeled “recurrent processing” or a central variable is called a “global workspace” without establishing the functional necessity of these features. Furthermore, existing studies typically focus on single theories in isolation (building a “GWT agent” [Goyal et al., 2022] or a “HOT-inspired Self-Model agent” [Wilterson and Graziano, 2021]), ignoring the potential interactions and dependencies between these mechanisms. Few studies subject these architectures to “adversarial phenomenology”: actively trying to break the system via lesions, noise, and deceptive signaling to distinguish genuine architectural advantages from mere task-specific overfitting.

In this work, we address these shortfalls by subjecting our agents to a battery of stress tests. We move beyond merely confirming theory predictions to stress-testing them in a controlled synthetic environment. To do this, we designed agents with reinforcement-learning-style architectures—trained here via supervised behavior cloning from an oracle (used only to generate training targets) to isolate architectural effects from optimization confounds—that incorporate specific architectural features proposed by consciousness theories. Specifically, we built agents with (1) a global workspace to broadcast information between modules (representing GWT), (2) a Self-Model to monitor internal states (representing HOT), and (3) complexity probes to measure information integration (inspired by IIT). Because these are software agents, we can perform manipulations that are impossible in biology: we apply causal lesions (selectively breaking parts of the “brain”), noise titration (injecting precise amounts of interference to test robustness), and adversarial reward structures (creating environments that incentivize the agent to “lie” to itself). Our findings reveal a functional hierarchy rather than competing theories:

1. Action Without Metacognition (Synthetic Blindsight): Consistent with HOT predictions, we find that in this agent family, ablating the Self-Model selectively abolishes metacognitive calibration (“knowing that you know”) while leaving first-order task performance largely intact, yielding a synthetic analogue of blindsight where agents can do without knowing.
1. Bus-Off Discontinuity in Access Markers: We observe an ignition-analogous discontinuity in this finite, discrete-capacity workspace: across the capacity settings we test, access markers remain similar across the tested non-zero capacities but collapse when the workspace is fully lesioned (bus-off)1 . Reducing workspace capacity does not gradually dim access within the tested levels; instead, a complete workspace lesion produces a qualitative collapse in access-related markers.
1. Broadcast-Amplification vs. Noise-Attenuation: Contrary to the intuition that broadcasting creates robustness [Baars, 1988, Bengio, 2017], we find that a global workspace alone exhibits a broadcast-amplification effect: it broadcasts information but also amplifies noise, making the system fragile even under standard regularization and noise augmentation. In our implementation, the B2 agent family remains robust in the same perturbation regime (L75 > 0.50), including in a Self-Model-off / workspace-read control; we therefore treat noise-attenuation as an empirical robustness property of the B2 family rather than as a bottleneck-only effect.
1. A Transfer Constraint on IIT-Adjacent Proxies: Raw perturbational complexity (PCI-A) is inverted under the workspace bottleneck: the GWT agent shows lower trajectory complexity than baselines, contrary to a naive “more integrated ⇒ higher PCI” expectation. This explicit negative result constrains how PCI-style measures transfer to engineered agents and suggests that absolute algorithmic complexity is not an architecture-invariant proxy for integration.

These results suggest that consciousness markers are not redundant. GWT provides the capacity for information exchange, while HOT mechanisms provide the control necessary to stabilize that exchange. Neither alone is sufficient for robust agency.

Scope and Limitations. Throughout this work, we focus strictly on Access Consciousness (information availability for report and action) rather than phenomenal consciousness or subjective experience. Our agents are not conscious; they are reference implementations of proposed mechanisms. Our claims concern functional correlates within these synthetic systems: whether certain architectural features are necessary or sufficient for particular behavioral and representational signatures. We make no claims about whether these features would produce phenomenal experience in biological or artificial systems. Because we evaluate up to n = 20 seeds per condition (Experiments 1–3; seed as the unit of analysis), our statistical claims are best viewed as proof-of-concept evidence; we highlight large qualitative effects and report uncertainty estimates for transparency. Some targeted sweeps and attribution controls are pilots (n = 5 seeds) and are labeled as such.

1Here, we use “ignition-analogous” in a loose access sense: an abrupt change between tested discrete capacity settings in a finite system. We do not claim a thermodynamic-limit phase transition, power-law scaling, or a precisely estimated critical point.

2 Background

Summary

이 섹션에서는 생물학적 이론과 합성 구현 사이의 격차를 해소하기 위해 본 연구에서 사용하는 주요 신경과학 용어를 명확히 정의한다. Type-1 성능은 주체의 결정 정확도(예: “자극이 왼쪽인지 오른쪽인지?“)를, Type-2 성능은 자신의 정확도를 모니터링하는 능력(예: “얼마나 확신하십니까?“)을 나타내며, 의식의 핵심 특징은 이 두 성능 간의 상관관계인 메타인지 민감도이다. 블라인드사이트와 같은 조건에서는 Type-1 성능이 높은 상태에서도 Type-2 인식이 부족할 수 있으며, 이는 실험 1에서 모델링된다. **점화(ignition)**와 **방송(broadcasting)**은 글로벌 워크스페이스 이론에 따르면 의식 접근이 비선형적인 임계점(점화)을 통해 발생하며, 이는 전두-두정망에서 지속적인 넓은 범위의 반향을 일으키는 과정이다. 이 과정의 정보 전달 제한은 병목 노드를 가진 버스 아키텍처로 모델링된다. 역방향 마스킹 실험에서는 짧은 자극-마스킹 간격(SOA)이 자극의 인식 가능성에 영향을 미치며, 시각 작업 기억은 인간에서 약 3~4개 항목의 제한적 용량을 가진 시스템으로, 마스킹 유사한 간섭과 용량 조절을 통해 합성 에이전트에서 유사한 동적을 검증한다. 베팅 패러다임은 주체가 자신의 결정 정확도에 베팅하는 방식으로, 올바른 선택 시 높은 베팅과 오류 시 낮은 베팅은 메타인지 보정을 나타내며, 선택 거절 옵션은 주관적 불확실성을 추가로 측정한다. 마지막으로 TMS-EEG와 **PCI(Perturbational Complexity Index)**는 뇌에 자극을 주고 EEG로 반응을 분석하여 의식 상태의 복잡성을 측정하는 기법이며, 본 연구에서는 합성 에이전트의 궤적에 대해 유사한 PCI-A 프록시를 적용한다.

2.1 Neuroscience & Consciousness Concepts

Summary

이 섹션에서는 생물학적 이론과 합성 구현 간 격차를 해소하기 위해 Type-1 성능과 Type-2 성능의 구분, Ignition 및 Broadcasting, Backward Masking, Visual Working Memory, Wagering Paradigm, TMS–EEG 및 PCI와 같은 핵심 신경과학 개념을 명확히 정의한다. Type-1 성능은 주체의 결정 정확도를, Type-2 성능은 자신의 정확도를 모니터링하는 능력을 나타내며, 두 성능 간의 상관관계인 메타인지 민감도는 의식의 핵심 특징으로, Blindsight와 같은 현상에서 Type-1 성능이 높은 상태에서도 Type-2 인식이 부족할 수 있음을 실험적으로 모델링한다. Global Workspace Theory에 따르면 의식 접근은 비선형 Ignition 이벤트를 통해 발생하며, 이는 Bottlenecked Bus Architecture를 통해 정보 유지 및 전파의 용량 한계를 테스트하는 방식으로 모델링된다. Backward Masking 실험은 자극과 마스크 간 시간 간격(SOA)에 따라 의식 접근의 시간적 역학을 탐구하며, Visual Working Memory는 인간의 3–4개 항목 수용 한계와 유사한 용량 제한을 가진 시스템으로, 마스킹과 용량 조작을 통해 합성 에이전트의 유사한 역학을 평가한다. Wagering Paradigm은 주체가 자신의 결정 정확도에 대한 베팅을 통해 메타인지 보정을 평가하는 방식으로, 합성 에이전트의 정확도에 대한 자신감을 캘리브레이션하는 능력을 검증한다. 마지막으로 **Perturbational Complexity Index (PCI)**는 TMS–EEG 기법을 통해 뇌의 알고리즘적 복잡성을 측정하는 지표로, 의식 상태에서는 복잡한 반응이 발생하는 반면 무의식 상태에서는 단순한 반응이 나타난다. 이를 모방한 PCI-A는 합성 에이전트의 경로에 유사한 변동-압축 논리를 적용하여 시뮬레이션한다.

To bridge the gap between biological theory and synthetic implementation, we clarify key neuroscientific terms used throughout this work.

Type-1 vs. Type-2 Performance. In psychophysics, Type-1 performance refers to the objective accuracy of a subject’s decision (e.g., “is the stimulus left or right?”). Type-2 performance refers to the subject’s ability to monitor their own accuracy, typically measured via confidence ratings (e.g., “how sure are you?”). A key signature of conscious awareness is the correlation between Type-1 and Type-2 performance (metacognitive sensitivity). Conditions like blindsight [Weiskrantz, 1986] demonstrate that high Type-1 performance can exist without Type-2 awareness, a dissociation we model in Experiment 1.

Ignition and Broadcasting. Global Workspace Theory posits that conscious access involves a nonlinear “ignition” event, an abrupt thresholding dynamic in which a stimulus overcomes a barrier to trigger sustained, widespread reverberation across fronto-parietal networks [Dehaene et al., 2006]. This “broadcasting” makes the information available to other cognitive processes. We model the capacitylimited broadcast aspect via a bottlenecked bus architecture; our implementation tests capacity constraints on information maintenance and broadcast, rather than competitive access gating.

Backward Masking and Visual Working Memory. Backward masking is an experimental technique in which a brief target stimulus is followed by a “mask” (a second stimulus) that interferes with conscious perception of the target. The stimulus-onset asynchrony (SOA), the time between target and mask onset, determines whether the target reaches awareness. This paradigm probes the temporal dynamics of conscious access. Visual working memory refers to the capacity-limited system that maintains visual information over short delays (typically 3–4 items in humans [Luck and Vogel, 1997, Cowan, 2001]). We use masking-like interference and capacity manipulations to test analogous dynamics in our synthetic agents.

Wagering Paradigms. A wagering or post-decision wagering paradigm asks subjects to bet on the correctness of their own decisions [Persaud et al., 2007]. High wagers on correct trials and low wagers on incorrect trials indicate good metacognitive calibration. An opt-out option (declining to wager) provides an additional measure of subjective uncertainty. We adapt this paradigm to assess whether our agents can calibrate confidence to their own accuracy.

TMS–EEG and PCI. The Perturbational Complexity Index (PCI) [Casali et al., 2013] is measured by perturbing the brain with transcranial magnetic stimulation (TMS, a non-invasive technique that induces neural activity via magnetic pulses) and recording the resulting spatiotemporal dynamics with electroencephalography (EEG, scalp recordings of electrical brain activity). PCI quantifies the algorithmic complexity of the brain’s response: conscious states produce complex, differentiated responses, while unconscious states (e.g., deep sleep, anesthesia) produce simpler, more stereotyped responses. Our PCI-A proxy applies an analogous perturbation-and-compress logic to synthetic agent trajectories.

Summary

이 섹션에서는 기존 연구와의 연계 및 확장을 중심으로, 본 연구가 기반을 둔 주요 연구 흐름을 정리한다. 먼저, 의식 기반 AI 아키텍처(Consciousness-Inspired AI Architectures)에 대해 다루며, GWT를 기반으로 한 재귀적 독립 메커니즘과 주의 기반 커뮤니케이션(Goyal et al., 2022), 시각 모델에서의 주의 게이트 전역 작업 공간(VanRullen et al., 2021), 그리고 HOT 기반의 명시적 자기 모니터링(Wilterson & Graziano, 2021) 등이 언급된다. 그러나 이들 연구는 일반적으로 단일 이론에 집중하고, 시스템적 Ablation 실험 없이 성능 향상만을 보인다는 한계가 있다. 본 연구는 (1) 여러 이론적 메커니즘을 통합한 아키텍처 구현, (2) 각 구성 요소의 시스템적 손상(lesion)을 통해 필수성을 검증, (3) 적대적 변동(adversarial perturbation)을 통해 진정한 안정성과 작업 특화 적합성의 차이를 분리하는 점에서 차별화된다.

메타인지와 정교정(Metacognition and Calibration in Machine Learning) 분야에서는 확률적 불확실성 측정과 정교정(calibration)이 다루어지며, 선택적 예측 프레임워크(Geifman & El-Yaniv, 2017)와 인간 유사한 메타인지와의 연관성(Raileanu & Fergus, 2020)이 언급된다. 본 연구의 Type-2 AUROC 지표는 이 분야에서 유래했으나, HOT 이론의 예측을 검증하기 위해 사용되며, 메타인지 정교정이 첫 번째 수준의 능력(first-order competence)에서 자동적으로 발생하는 것이 아니라 두 번째 수준의 자기 표현(higher-order self-representation)이 필요하다는 가설을 검증한다. 이에 따라 자기 인식이 유지되면서 메타인지가 파괴된 합성 맹시(synthetic blindsight) 실험은 이 가설의 통제된 테스트 케이스로 활용된다.

신경망의 안정성과 노이즈(Robustness and Noise in Neural Networks) 분야에서는 적대적 변동(Szegedy et al., 2014)과 분포 이동(distribution shift)에 대한 연구가 언급되며, 노이즈 주입(Srivastava et al., 2014)과 표현 기하학(Mahloujifar et al., 2019)의 분석이 소개된다. 본 연구의 브로드캐스트 증폭(broadcast-amplification) 발견은 이와 연계되나, 입력 노이즈(input noise)가 아닌 워크스페이스 내 잠재 노이즈(latent perturbation)에 초점을 맞추며, 브로드캐스트만으로 노이즈가 증폭되는 현상을 보인다. 이에 비해 B2 아키텍처(B2 family)는 동일한 잠재 노이즈 환경에서도 안정성을 보이며, 입력 수준 방어(input-level defense)를 넘어 추가적인 아키텍처 구조와 훈련 목적(training objective)이 보완적 안정성 메커니즘을 제공할 수 있음을 시사한다.

마지막으로, 강화 학습에서의 메타인지(Metacognition in Reinforcement Learning) 분야에서는 불확실성 측정(Guo et al., 2017)을 기반으로 한 메타인지 모니터링이 변동 내성(perturbation tolerance) 향상에 기여함을 보여주는 연구(Anderson & Oates, 2020)와 신뢰도 편향(confidence bias)이 강화 학습의 학습 역학에 직접적인 영향을 미친다는 주장(Salem-Garcia et al., 2023)이 언급된다. 본 연구는 이와 달리 아키텍처 손상(architectural lesion)을 통해 첫 번째 수준의 성능(first-order performance)과 두 번째 수준의 신뢰도(second-order confidence)를 인과적으로 분리함으로써, 작업 능력과 메타인지 간 계층적 관계를 주장하는 이론(Fleming, 2024)에 대한 합성 실험 환경(synthetic testbed)을 제공한다.

Our work builds on and extends several research threads that have previously remained largely separate.

Consciousness-Inspired AI Architectures. Several recent efforts have sought to implement consciousness-related mechanisms in artificial systems. Goyal et al. [2022] introduced recurrent independent mechanisms with attention-based communication, inspired by GWT’s broadcast architecture. VanRullen et al. [2021] explored attention-gated global workspaces in vision models. Wilterson and Graziano [2021] developed HOT-inspired architectures with explicit self-monitoring. However, these works typically focus on single theories in isolation and demonstrate performance gains without systematic ablation or stress-testing to establish causal necessity. Our contribution is to (1) implement multiple theoretical mechanisms within a unified architecture, (2) systematically lesion each component to establish necessity, and (3) subject the system to adversarial perturbations that distinguish genuine robustness from task-specific fitting.

Metacognition and Calibration in Machine Learning. The machine learning literature has extensively studied uncertainty quantification and calibrated confidence [Guo et al., 2017]. Selective prediction frameworks [Geifman and El-Yaniv, 2017] allow models to abstain when uncertain, and recent work connects these ideas to human-like metacognition [Raileanu and Fergus, 2020]. Our Type-2 AUROC metric derives from this literature but is deployed here to test HOT-specific predictions: that metacognitive calibration requires a higher-order self-representation rather than emerging automatically from first-order competence. The synthetic blindsight dissociation we report (preserved task performance with abolished metacognition) provides a controlled test case for these ideas.

Robustness and Noise in Neural Networks. The fragility of deep networks to adversarial perturbations [Szegedy et al., 2014] and distribution shift [Hendrycks and Dietterich, 2019] is well documented. Prior work has explored noise injection during training for regularization [Srivastava et al., 2014] and studied the geometry of learned representations under perturbation [Mahloujifar et al., 2019]. Our broadcast-amplification finding connects to this literature but focuses on latent perturbations (noise in the workspace, not inputs) and demonstrates that broadcasting alone amplifies rather than filters noise. The B2 family’s robustness in the same latent-noise regime suggests that additional architectural structure and training objectives can provide complementary robustness mechanisms beyond input-level defenses.

Metacognition in Reinforcement Learning. While uncertainty quantification in deep learning is well-established [Guo et al., 2017], recent work has begun to explore the functional role of metacognition in reinforcement learning agents. Anderson and Oates [2020] demonstrated that metacognitive monitoring can enhance perturbation tolerance in RL agents, a finding consistent with our noise-attenuation hypothesis. Similarly, Salem-Garcia et al. [2023] linked confidence biases to fundamental RL processes, suggesting that miscalibration is not merely a post-hoc artifact but can actively shape learning dynamics. Our work extends these perspectives by causally dissociating first-order performance from second-order confidence via architectural lesions, providing a synthetic testbed for theories that posit hierarchical relationships between task competence and metacognitive awareness [Fleming, 2024].

3 From Theories to Synthetic Indicators

Summary

이 섹션에서는 이론적 개념을 합성 에이전트 내에서 측정 가능한 지표로 변환하는 핵심 과제를 다룬다. Higher-Order Theories (HOT), Global Workspace Theory (GWT), **Integrated Information Theory (IIT)**의 세 주요 이론 클러스터를 선택해 각각의 기능적 차원(모니터링, 접근, 통합)에 대응하는 합성 지표를 설계했다. HOT은 시스템이 자신의 상태를 인식하는 **Self-Model (zself)**을 구현하고, Type-2 AUROC을 통해 메타인지 보정 능력을 평가하며, 이를 **실험 1 (E1)**에서 첫 번째 차원(행동)과 두 번째 차원(의식)의 분리 가능성을 검증한다. GWT는 전역 정보 접근을 위해 경로 제한된 버스 아키텍처를 도입하고, **Ignition (작업 공간 활성화의 급격한 증가)**와 **Global Broadcast Index (GBI)**를 핵심 지표로 설정해 **실험 2 (E2)**에서 정보 접근의 인과적 기반을 탐구한다. IIT는 정보 통합 능력을 Φ로 측정하지만, 대신 PCI (Perturbational Complexity Index) 유사한 Trajectory Complexity를 사용해 인공 시스템에서의 전이 가능성을 평가한다. 특히, **PCI-A (절대적 트래잭토리 복잡도)**와 **ΔPCI (정확한 시도와 오류 시도 간 복잡도 차이)**를 통해 아키텍처 변화에 따른 복잡성의 단조로운 변화를 분석하며, **실험 3 (E3)**에서 이 지표들이 합성 시스템 내에서 어떻게 작동하는지 검토한다. 이 지표들은 각 이론에 대응하는 구체적인 프로파일을 형성하며, 이는 표 1에 요약되어 있다.

Having established the relevant neuroscientific terminology and experimental paradigms, we now turn to the core challenge of this work: translation. To move beyond loose analogies between brains and machines, we must operationalize theoretical constructs into precise, measurable indicators within our synthetic agents. We selected three dominant clusters of consciousness theories (HOT, GWT, and IIT) because they address distinct functional facets of consciousness that are often conflated: (1) Monitoring (reflexive awareness), (2) Access (information availability), and (3) Integration (phenomenological unity). By testing these pillars individually, we can determine whether they are redundant or complementary.

Higher-Order Theories (HOT). HOT suggests that a state is conscious only when the system represents itself as being in that state [Rosenthal, 2005, Lau and Rosenthal, 2011]. This corresponds to the Monitoring dimension: access alone is insufficient for confidence, error correction, and a “personal” perspective. We implement this via a dedicated Self-Model (zself) that compresses the workspace state into a summary latent. The indicator is Metacognitive Calibration (Type-2 AUROC), measuring the system’s ability to “know that it knows” [Fleming et al., 2010]. We test this in Experiment 1 to dissociate doing (first-order performance) from knowing (second-order awareness).

Global Workspace Theory (GWT). GWT posits that consciousness arises from a global broadcast mechanism where information from specialized modules is selected and amplified (“ignited”) for systemwide access [Baars, 1988, Dehaene and Changeux, 2011]. This corresponds to the Access dimension: without global broadcasting, there is no “content” to be conscious of. In our agents, we operationalize this as a bottlenecked bus architecture. The key indicators are Ignition, a sudden, non-linear jump in workspace activation, and the Global Broadcast Index (GBI), quantifying the extent of information sharing across the system. We test this in Experiment 2 to establish the causal substrate of information access.

Integrated Information Theory (IIT). IIT argues that consciousness corresponds to the capacity of a system to integrate information, measured as $Φ$ [Tononi, 2004, Oizumi et al., 2014]. This corresponds to the Integration dimension: consciousness is characteristically unified and differentiated.

We do not compute $Φ$ directly. Instead, we include a PCI-inspired perturbational complexity probe [Casali et al., 2013] as a transfer test: if “PCI-like” trajectory complexity were a broadly architecture-invariant proxy for IIT-style integration, then architectures that enforce more global coupling and causal interdependence should tend to exhibit higher perturbation-evoked complexity.

However, in engineered agents this expectation is not guaranteed [Shwartz-Ziv and Tishby, 2017, Ansuini et al., 2019]. In particular, a global workspace can behave as a bottleneck and organizer: by forcing many downstream computations to depend on a shared, low-rank broadcast state, it can increase redundancy and push dynamics onto a lower-dimensional manifold. Under such conditions, stronger architectural “integration” (in the everyday engineering sense of tighter coupling) can plausibly produce lower Lempel–Ziv compressibility-based trajectory complexity.

Accordingly, we treat raw PCI-A as a falsifiable probe rather than a confirmatory marker, and we interpret deviations (including inversions) as informative constraints on how PCI-style measures do or do not transfer to artificial systems. We report both raw PCI-A (absolute post-perturbation trajectory complexity) and a contrastive measure, $Δ$ PCI (correct minus incorrect trial complexity), which aims to partially control for the fact that in these agents, “complexity” can be inflated by unstructured failure/noise. We include this in Experiment 3 to test which aspects of PCI-style proxies behave monotonically with architectural changes in this synthetic setting.

These indicators form a distinct profile for each theory, summarized in Table 1.

Table 1. Mapping theoretical clusters to symmetre indicators and experiments.
Exp.	Theory Cluster	Intended Property	Synthetic Indicator
E1	HOT / Self-Model	Metacognitive access	Type-2 AUROC, $z_{self}$ lesion
E2	GWT	Global access, ignition	GBI, Ignition Sharpness
E3	Complexity probe (IIT-adjacent)	Richness, differentiation	PCI-A (raw), $Δ$ PCI
E3	Composite	Joint “conscious-like” profile	$Reduced composite (GBI +$
			$Δ$ PCI); full CTS adds AU-
			ROC

Table 1: Mapping theoretical clusters to synthetic indicators and experiments.

4 Methods

Summary

이 섹션에서는 의식 이론을 기반으로 한 다양한 에이전트 아키텍처를 비교하는 방법론을 제시한다. 모든 에이전트는 $O_{g r i d} \in N^{7 \times 7 \times 3}$ 입력을 처리하는 공통된 Convolutional Encoder(3-layer CNN)를 사용하지만, 고위 단계 인지 모듈에서 차이를 보인다. **Feedforward Baseline (A0)**은 단순히 MLP 정책 헤드를 연결한 반응형 에이전트로, 시간적 통합을 요구하는 작업에서는 제한적인 성능을 보인다. **Recurrent Baseline (A1)**은 GRU(64 hidden units)를 통해 내부 상태를 유지하지만, Global Workspace Theory (GWT) 기반의 **GWT Agent (B1)**은 제한된 용량의 Workspace Bus(K=4, D=16)를 통해 정보를 저장하고 전달하는 메커니즘을 도입한다. **Self-Model Agent (B2)**는 HOT 이론을 반영해 Self-Model (zself) 모듈을 추가해 고차원 정보를 압축하고, 정책 실행 시 Type-2 성능(메타인지 민감도)을 평가하는 Confidence Head를 구현한다. 실험적으로 Workspace Lesion(K=0)과 Compression Control(PCA 기반)을 통해 Broadcast와 Self-Modeling의 역할을 분리해 평가하며, Denoising Attribution Baseline을 통해 HOT-only와 BC-only 조건에서의 안정성을 비교한다. 특히, Type-2 AUROC이 무작위 수준으로 떨어지는 실험 결과는 Self-Model의 부재가 메타인지 능력을 완전히 상실시킨다는 점을 강조한다.

4.1 Architectures

Summary

이 섹션에서는 의식 이론에 기반한 다양한 에이전트 아키텍처를 비교하는 핵심 실험을 다룬다. 모든 에이전트는 공통된 백본(3층 CNN을 통해 7×7×3 입력을 151차원 관찰 임베딩으로 변환)을 공유하지만, 고위 인지 모듈에서 차이를 보인다. Feedforward 기준선(A0)은 메모리 없이 직접 시각 인코더에 연결된 MLP 정책 헤드로 구성된 순수 반응형 에이전트이며, Recurrent 기준선(A1)은 64개의 은닉 단위를 가진 GRU를 통해 기억을 처리하는 표준 강화학습 에이전트다. GWT 에이전트(B1)는 제한된 용량의 워크스페이스 버스(K=4, D=16)를 도입해 메모리 슬롯에 쓰기 및 읽기 메커니즘을 적용하고, 용량 조절(K=0으로 완전한 손상 실험)을 통해 의식 마커의 영향을 분석한다. HOT 기반 Self-Model 에이전트(B2)는 B1에 자기 모델(zself, 64차원 압축된 잠재 범용 병목)을 추가해 정책 라우팅을 조절하며, 메타인지 민감도 평가 실험(Experiment 1)에서는 zself를 통한 정책 실행을 비활성화해 Type-2 성능을 테스트한다. 또한, 기여도 분리를 위해 B2를 K=0 상태에서 평가하거나 PCA 기반 압축 기준선과 비교해, 자기 모델의 학습된 내용이 메타인지 정보에 필수적임을 보인다. 마지막으로 노이즈 내성 실험(Experiment 3)에서는 HOT-only(워크스페이스 없이 zself만 사용) 및 BC-only(워크스페이스 상태로 직접 압축) 기준선을 도입해, 저차원 병목의 일반적 효과와 자기 모델의 특이한 내성 향상 차이를 분석한다.

We compared a hierarchy of agent architectures, all sharing a common backbone but differing in their high-level cognitive modules.

Common Backbone. All agents use a convolutional encoder (3-layer CNN) to process the $O_{g r i d} \in N^{7 \times 7 \times 3}$ input, producing a 151-dimensional observation embedding.

Feedforward Baseline (A0). A purely reactive agent consisting of an MLP (Multi-Layer Perceptron) policy head attached directly to the visual encoder. It lacks memory or internal state, serving as a control for tasks requiring temporal integration.

Recurrent Baseline (A1). A standard recurrent agent where the observation embedding feeds into a Gated Recurrent Unit (GRU) with 64 hidden units. The policy head reads directly from the GRU hidden state. This represents the “status quo” of deep reinforcement learning agents—capable of memory but lacking explicit workspace or Self-Model structures.

GWT Agent (B1): The Global Workspace. This agent implements a capacity-limited broadcast mechanism.

• Workspace Bus: A set of K memory slots (default K = 4, dimension D = 16).

Write Mechanism: Recurrent state features are projected to a write vector and stored in the fixed-capacity buffer. At each step, the write vector is placed into the first available empty slot; if all slots are occupied, a fixed slot (slot 0) is overwritten.2 This deterministic allocation tests capacity limitation and broadcast, not competitive attention-based access gating.
Broadcast (Read): The content of all slots is aggregated and broadcast back to the policy head. We use a flattened-readout MLP that concatenates all workspace slots into a single vector and projects through a multi-layer network to produce action logits.
Capacity Control: We can manipulate the number of active slots K (full capacity K = 4, intermediate reductions, and K = 0 (bus-off) for a complete lesion).

Self-Model Agent (B2; HOT-inspired). This agent extends B1 by adding a higher-order monitoring system.

Self-Model (zself): A secondary module that does not directly see the world. Instead, it observes the workspace broadcast (a D-dim summary), the recurrent carrier state, and the agent’s own intended actions (policy logits).
Compression: It compresses this high-dimensional input (89 dims: 64-d recurrent carrier + 16-d workspace broadcast + 7 action logits + 2 uncertainty scalars) into a tiny latent bottleneck (zself, dim=64, effectively lower due to regularization).
Policy Routing: The confidence head (for wagering) reads exclusively from zself. The action policy routing varies by experiment: in Experiment 1 (metacognition), the action policy reads directly from the workspace (not zself) so that Self-Model lesions preserve first-order performance while abolishing metacognition. In Experiment 3 (noise robustness), we evaluate both configurations: a “workspace-read” control where the action policy bypasses zself, and the standard B2 where the action policy reads from zself.

Baseline Variants for Disentangling Contributions. Two controls help separate the roles of broadcast and self-modeling. (i) We evaluate B2 with the Self-Model enabled under a complete workspace lesion (bus-off; K = 0), which tests whether a monitor can produce spurious metacognition when its monitored substrate is absent; Type-2 AUROC collapses to chance (see Experiment 1). (ii) We include compression and pathway controls: blind ablations (noise/permutation) and a PCA baseline matched to the effective dimensionality of zself to show that metacognitive information depends on the learned content of zself, not merely on the presence of a bottleneck.

Denoising attribution baselines (Experiment 3 controls). To tighten attribution for the robustness effects in Experiment 3, we additionally evaluate two baseline families. First, a “HOT-only” agent (A1 + zself without any workspace bus) tests whether a Self-Model bottleneck can improve robustness in the absence of a broadcast substrate. Because this agent has no workspace bus, it cannot be evaluated under the strong-lesion cue routing (cues-to-workspace-only), so cues remain visible in its observation stream; we probe robustness by injecting noise into the recurrent carrier state (post-GRU hidden state) rather than into workspace slots. Second, we include matched “BC-only” compressor controls that replace zself with a 64-d bottleneck applied directly to the flattened workspace state (linear projection, small MLP, and fixed random projection). These controls distinguish a Self-Model-specific robustness gain from a generic benefit of adding a low-dimensional bottleneck; results are summarized in Figure 4.

4.2 Environments

Summary

이 섹션에서는 의식 이론을 검증하기 위해 설계된 합성 환경(synthetic environments)의 구조와 실험 설계를 설명한다. 모든 실험은 MiniGrid 기반의 맞춤형 2D 그리드월드 환경에서 수행되었으며, 에이전트는 7×7 그리드로 구성된 로컬 뷰를 통해 세계를 인식하고 이동, 회전, 물건 수거 등의 이산 행동을 수행한다. 관찰 공간은 객체 ID, 색상, 상태 정보를 포함하는 Ogrid ∈ N 7×7×3 텐서와 작업 특화 벡터로 구성된다. Wagering Paradigm(실험 1)에서는 메타인지(metacognition)를 평가하기 위해, 에이전트가 가변적 명확도를 가진 자극을 분류한 후 연속적인 신뢰도 신호(continuous confidence signal)를 출력하도록 설계되었으며, 높은 신뢰도(>0.5)는 +1 보상, 낮은 신뢰도(≤0.5)는 0 보상을 제공한다. Dual-Task Paradigm(실험 2)에서는 GWT 예측을 검증하기 위해, 두 개의 일시적 자극을 인코딩-유지-보고하는 세 단계 구조를 도입했으며, 워크스페이스 버스(workspace bus)를 통해만 정보가 전달되도록 강한 손상(strong-lesion) 설계를 적용했다. 마지막으로, Latent Noise Stress Test(실험 3)에서는 내부 워크스페이스 슬롯(internal workspace slots)에 가우시안 노이즈를 주입하여 시스템의 안정성을 평가했으며, L75(75% 정확도 유지 가능한 최대 노이즈 수준)를 지표로 사용해 인지 아키텍처의 내구성(tolerance margin)을 정량화했다.

All experiments were conducted within customized MiniGrid environments [Chevalier-Boisvert et al., 2018], a standard 2D gridworld framework where agents perceive the world through a local view (7 × 7 grid) and take discrete actions (move forward, turn left, turn right, pick up, drop, toggle, done). The observation space consists of a symbolic tensor Ogrid ∈ N 7×7×3 (object ID, color, state) plus a task-specific vector.

2We use fixed-slot overwrite rather than true FIFO (evicting the oldest entry) for implementation simplicity. In our short-episode tasks (32 steps) with sparse cue-write events, the workspace rarely fills completely, so the fallback policy seldom activates. When it does, the flattened-readout architecture ensures all slot contents remain accessible to the policy regardless of which slot was overwritten. This design choice therefore does not affect the validity of our capacity-limitation experiments.

Wagering Paradigm (Experiment 1). To assess metacognition, we implemented a wagering task within the MiniGrid framework. The agent navigates to a “stimulus zone” where a transient cue (encoded via the standard MiniGrid observation channels) appears with variable salience (simulating perceptual uncertainty). The agent must then navigate to one of two “response zones” to indicate its classification.

Task: Classify which of two cue types (s ∈ {0, 1}) was presented, where cue salience is degraded by observation noise.
Wager: On 50% of trials, a “wager flag” appears after the decision, prompting the agent to output a continuous confidence signal c ∈ [0, 1] via a dedicated action channel.
Reward Structure: High confidence (c > 0.5) counts as a “bet” (+1 reward for correct, -1 for incorrect). Low confidence (c ≤ 0.5) counts as an “opt-out” (0 reward). This incentivizes the agent to align its internal confidence c with its objective probability of correctness P(correct).

Dual-Task Paradigm (Experiment 2). To test GWT predictions, we used a MiniGrid-Empty-5x5-v0 variant with a dual-task structure. Each episode (max 32 steps) involves:

1. Encoding Phase: Agents observe two transient cues: a “secondary” cue (color) and a “primary” cue (object type).
1. Delay Phase: Agents must navigate the empty room while maintaining both cues in working memory.
1. Report Phase 1 (Early): A specific “report flag” signal triggers the agent to output the secondary cue.
1. Report Phase 2 (Late): A second flag triggers the agent to output the primary cue.

We employed a “strong-lesion” wiring: cue information was routed exclusively through the workspace bus, while the standard recurrent encoder was blind to these specific cue channels. This ensures the workspace is the sole causal pathway for task-relevant information.

Latent Noise Stress Test (Experiment 3). To evaluate robustness on the dual-task paradigm (Experiment 2), we introduced a Latent Workspace Perturbation protocol. Instead of adding noise to the pixel observations (which traditional CNNs can easily filter), we injected Gaussian noise N (0, σ2 ) directly into the agent’s internal workspace slots immediately after the write operation but before the read operation. For recurrence-only controls without a workspace (HOT-only), we analogously inject Gaussian noise into the recurrent carrier state (post-GRU hidden state) immediately after the recurrent update and before downstream readouts. This “brain stimulation” approach tests the system’s stability against internal degradation. We measured the L75: the noise level σ at which report-step decision accuracy drops to 75%.3 This effectively quantifies the “tolerance margin” of the cognitive architecture.

4.3 Training

Summary

이 섹션에서는 에이전트의 기초 능력 확보를 위해 Behavior Cloning (BC) 방식을 사용해 전문가 오라클로부터 학습시킨 점을 설명한다. BC는 강화학습(RL)에 나타나는 탐색 실패, 보상 희소성, 학습 불안정성 등의 문제를 줄여, 모듈 조작(lesions)과 변동성(perturbations)에 따른 차이가 아키텍처 조정에 기인함을 보장하기 위해 채택되었다. 오라클은 학습 중 행동 타겟 생성에만 활용되며, 추론 단계에서는 절대 참조되지 않는다. 평가 과정은 학습된 정책의 자율적 롤아웃을 통해 수행되며, 핵심 결과는 학습 후 인과적 간섭(lesions, capacity ablations, latent workspace noise)을 통해 도출된다. 이 프레임워크는 기초 능력을 달성한 에이전트를 전제로, 접근성 및 메타인지 관련 특징(access- and metacognition-related signatures)을 형성하는 데 인과적으로 필수적인 구성 요소는 무엇인지를 탐구하는 조건부 주장으로 이어진다. 또한, L75이라는 용어를 사용해 독성학에서의 LD50(50% 치사량)과 혼동을 피하고, 75% 정확도를 기준으로 설정한 점도 강조된다.

Agents were trained using Behavior Cloning (BC) from an expert oracle to ensure baseline competence. We use BC as an optimization control: it reduces RL-specific confounds (exploration failures, reward sparsity, and training instability) so that differences under lesions and perturbations can be attributed to architectural manipulations rather than optimization dynamics. The oracle is used only to generate action targets during training; it is never consulted at inference. All evaluations are autonomous rollouts of the learned policy, and our central results are established via post-training causal interventions (lesions, capacity ablations, and latent workspace noise) applied to trained agents. This framing makes our claims conditional: given agents that reach baseline first-order competence, which components are causally necessary for access- and metacognition-related signatures?

3We use “L75” rather than “LD50” to avoid confusion with the toxicology convention where LD50 denotes the dose causing 50% lethality. Our threshold uses 75% accuracy (not 50% accuracy).

4.3.1 Training Procedure

Summary

이 섹션에서는 합성 환경에서 에이전트를 훈련시키기 위한 훈련 절차(Training Procedure)를 상세히 설명한다. 데이터셋 생성은 Oracle(완벽한 환경 역학과 작업 규칙을 알고 있는 하드코드 알고리즘)을 기반으로 하여, 각 에이전트 유형과 시드에 대해 최대 32단계의 환경 스텝을 포함한 에피소드를 수집하였다. 손실 함수(Loss Function)는 에이전트의 예측 행동 분포 $π_{θ} (a ∣ s)$ 와 Oracle의 분포 $π^{*} (a ∣ s)$ 간 KL 발산(Kullback-Leibler Divergence)을 최소화하는 방식으로 정의되었으며, 수식으로는 $L_{BC} = E_{s \sim D} [D_{KL} (π^{*} (a ∣ s) ∣∣ π_{θ} (a ∣ s))]$ 로 표현된다. 최적화(Optimization)는 Adam 최적화기( $β_{1} = 0.9$ , $β_{2} = 0.999$ )를 사용해 학습률 $1 0^{- 3}$ 로 진행되었으며, 온라인 훈련(각 에피소드를 즉시 처리)을 통해 순환 상태의 시간적 일관성을 유지하였다. 수렴 기준(Convergence Criteria)은 훈련 종료 시 보류된 에피소드(held-out episodes)에서 에이전트의 Oracle 행동과의 일치율이 95%를 초과하는지 확인하는 방식으로 설정되었으며, 이 임계값을 충족하지 못한 시드는 분석에서 제외되었다.

Dataset Generation. We generated training data using a hard-coded algorithmic solver (the “Oracle”) that has perfect knowledge of the environment dynamics and task rules. For each experiment, we collected oracle demonstrations per agent type and seed (see Table 2 for episode counts by experiment). Each episode consists of up to 32 environment steps. The Oracle’s action at each step was recorded as the target distribution for behavior cloning.

Loss Function. We minimized the Kullback-Leibler (KL) divergence between the agent’s predicted action distribution πθ(a|s) and the oracle’s action distribution π ∗ (a|s):

$L_{BC} = E_{s \sim D} [D_{KL} (π^{*} (a ∣ s) ∣∣ π_{θ} (a ∣ s))]$

where D is the dataset of oracle demonstrations.

Optimization. Training proceeded for the number of episodes specified in Table 2 (with one optimizer update per step) using the Adam optimizer [Kingma and Ba, 2014] with default momentum parameters (β1 = 0.9, β2 = 0.999). The learning rate was set to 10−3 for all agents. We used online training (processing each episode immediately rather than batching across episodes) to maintain temporal coherence of recurrent states. No learning rate scheduling or warm-up was employed.

Convergence Criteria. Training was run for a fixed number of episodes rather than early stopping, as behavior cloning from a deterministic oracle converges reliably. We verified convergence by confirming that agents achieved >95% oracle-action agreement on held-out episodes (per-step argmax match) by the end of training. Seeds that failed to reach this imitation threshold were flagged and excluded from analysis.

4.3.2 Stabilization Techniques

Summary

이 섹션에서는 듀얼-태스크 패러다임의 학습 과정에서 발생하는 두 가지 주요 문제, 즉 시간적 클래스 불균형(report step이 전체 단계의 약 3%에 불과한 점)과 Self-Model의 직접 감독 없이 의미 있는 표현 학습의 필요성을 해결하기 위한 기법을 제시한다. 첫째, Report-Step Reweighting을 통해 report step의 KL 손실을 3.0배로 가중치 조정하고, “primary cue” 행동에 대해 “secondary cue”보다 20배 높은 가중치를 부여하여 희귀한 신호의 영향력을 강화했다. 둘째, 메타인지 감독(B2 에이전트에 적용)을 통해 report step에서의 이진 정확도를 예측하는 보조 손실 $L_{m e t a} = BCE (c, \hat{1}_{correc t})$ 를 추가함으로써 에이전트의 실패 모드에 대한 보정을 가능하게 했으며, 이는 Self-Model(zself)이 메타인지 판단에 직접 관여하도록 설계했다. 마지막으로, 자극 보조 손실은 지연 기간 동안 작업 공간의 자극 정보를 유지하기 위해 workspace 상태로부터 자극 존재 여부를 예측하는 선형 프로브를 학습시켜, report 시점 전에 메모리 흔적이 퇴색하지 않도록 밀집된 기울기 정보를 제공한다.

The dual-task paradigm creates two challenges for training: (1) temporal class imbalance, where report steps constitute only ∼3% of all steps, and (2) the need for the Self-Model to learn meaningful representations without direct supervision. We addressed these with targeted interventions:

Report-Step Reweighting: Report steps are rare but critical for evaluation. To prevent these sparse signals from being dominated by navigation steps, we upweighted the KL loss on report steps by a factor of 3.0. Additionally, we applied class-specific weighting: the “primary cue” action (correct on only ∼5% of steps) received 20× higher weight than the “secondary cue” action in the loss computation.
Metacognitive Supervision (B2 agents; Experiments 1 and 3): For B2 agents, we added a supervised auxiliary loss training the confidence head to predict binary correctness on report steps: Lmeta = BCE(c, ˆ 1correct), where cˆ is the agent’s confidence output. Here, 1correct is defined by the agent’s own intended report decision (argmax of its policy logits) being correct, as assessed against the oracle-provided ground-truth label at that report step. This trains calibration on the agent’s own failure modes (“will my imminent decision be correct?”) rather than on predicting oracle behavior. This places the Self-Model (zself) directly in the gradient path for metacognitive judgments.
Stimulus Auxiliary Loss (Experiment 1 only): To ensure the workspace maintains stimulus information throughout the delay period, we added an auxiliary loss training a linear probe on the workspace state to predict stimulus presence at every step, not just report steps. This provides dense gradients that prevent the workspace memory trace from fading before the critical report moment.

4.3.3 Validation Strategy

Summary

이 섹션에서는 held-out validation 전략을 통해 모델의 일반화 능력을 평가한 점을 설명한다. 훈련 데이터는 E1/E2의 경우 4,000개, E3의 경우 8,000개의 오라클 에피소드로 구성되었고, 검증은 다른 랜덤 시드로 생성된 독립적인 에피소드(Experiment 2에서는 시드당 32개, robustness 실험에서는 노이즈 수준당 50개)에서 수행되었다. 평가 지표로는 oracle-action agreement(모방 정확도)와 conjunction accuracy(두 report 단계 모두 정확한 경우), report-window decision accuracy 등을 사용했으며, held-out 데이터에서 95% 이상의 oracle-action agreement를 달성해야 훈련 성공으로 간주하였다. 또한, 하이퍼파라미터 튜닝은 테스트 데이터에 적용되지 않았고, 평가에 사용된 에피소드는 하이퍼파라미터 선택 과정에서 전혀 활용되지 않았다.

We employed a simple held-out validation approach:

• Train/Test Split: After training on the specified number of oracle episodes (4,000 for E1/E2; 8,000 for E3; see Table 2), we evaluated agents on held-out independently sampled episodes with

different random seeds (Experiment 2 capacity sweeps use 32 episodes per seed; robustness titrations use 50 episodes per noise level). These held-out episodes used the same task structure but different initial conditions and cue assignments.

Metrics: Validation performance was assessed via oracle-action agreement (imitation accuracy) and task-level scores such as conjunction accuracy (both report phases correct) and report-window decision accuracy. We required >95% oracle-action agreement on held-out data to consider training successful.
No Hyperparameter Tuning on Test Data: All hyperparameters were fixed before evaluation. The evaluation episodes used for reporting results (Experiments 1–3) were never used during hyperparameter selection.

4.3.4 Hyperparameter Selection

Summary

이 섹션에서는 하이퍼파라미터 선택 과정을 설명하며, 이론 기반의 사전 지식과 제한된 수동적 탐색을 결합해 결정했다고 밝힌다. Workspace 용량(K=4 슬롯, D=16 차원)은 인간의 시각 작업 기억 용량 추정치를 기반으로 설정했으며, Self-Model의 잠재 차원(64)은 작업 공간 상태(K×D=64)와 동일하거나 작게 유지되도록 조정했다. 학습률(10⁻³)은 안정성 없이 가장 빠르게 수렴하는 값을 선택했고, 손실 가중치(Report-step 가중치 3.0, 주요 클래스 가중치 20.0)는 희귀한 단계 유형의 영향력을 균형 있게 반영하도록 설정했다. 자동화된 탐색(그리드/랜덤/베이지안 최적화)은 사용하지 않았으며, 이는 아키텍처 가설 검증에 집중하기 위한 선택이었다. 표 2는 실험별 주요 하이퍼파라미터를 정리해 보여주며, 모든 실험은 Adam 최적화기와 기본 모멘텀 설정을 사용했다.

Hyperparameters were selected through a combination of theory-driven priors and limited manual search:

Architecture: Workspace capacity (K = 4 slots) and dimension (D = 16) were chosen to match estimates of human visual working memory capacity [Luck and Vogel, 1997, Cowan, 2001]. The Self-Model latent dimension (64) was set to allow sufficient representational capacity while remaining no larger than the workspace state (K × D = 64).
Learning Rate: We tested {10−4 , 10−3 , 10−2} on a single seed and selected 10−3 based on fastest convergence without instability. This choice was fixed for all subsequent experiments.
Loss Weights: The report-step reweighting factor (3.0) and class weight (20.0) were selected to approximately balance the contribution of rare and common step types to the total loss. We did not extensively tune these values.
No Automated Search: We did not employ grid search, random search, or Bayesian optimization. The limited hyperparameter exploration reflects our goal of testing architectural hypotheses rather than maximizing benchmark performance.

Table 2 summarizes the key hyperparameters used across experiments.

Table 2: Training hyperparameters by experiment. All experiments used Adam optimizer with default momentum.

	Steps per episodeLearning rateWorkspace slots K	3210−34	3210−34 (varied)	3210−34
	Report step weight	3.0	3.0	3.0
Self-Model dim64—64	Primary class weightMeta-loss coefficient	20.01.0	20.0—	20.01.0
	Random seeds	20	20	20

4.4 Indicator Computation

Summary

이 섹션에서는 의식 이론을 검증하기 위한 핵심 지표 계산 방법을 제시한다. 먼저, **Global Broadcast Index (GBI)**는 workspace 슬롯 간 정보 공유의 범위를 측정하기 위해 참여 계수 기반의 지표로, 각 슬롯의 활성화 벡터 간 유사도를 기반으로 adjacency matrix를 정의하고, 이를 통해 계산된 참여 계수의 평균을 사용한다. Ignition Sharpness는 workspace 활성화의 급격한 증가를 탐지하기 위해 활성화 노름의 시간 도함수와 피크의 급격함을 측정하며, 이는 의식의 “점화” 현상과 유사한 전이를 나타낸다. Type-2 AUROC은 에이전트의 메타인지 능력을 평가하기 위해, 신뢰도를 정확도의 예측자로 사용해 ROC 곡선 하부 면적을 계산하며, 0.5는 우연, 1.0은 완벽한 인식을 의미한다. **Perturbational Complexity (PCI-A, ∆PCI)**는 IIT와 유사한 통합 지표를 탐색하기 위해 workspace에 노이즈를 주입한 후 상태 변화를 추적하고, Lempel–Ziv 압축 알고리즘을 통해 압축된 파일 크기를 기반으로 알고리즘적 복잡도를 측정하며, ∆PCI는 성공/실패 시험 간 복잡도 차이를 비교한다. 마지막으로, **No-Report Signature (∆NRS)**는 보고가 차단된 동안 자극 정보가 내부 상태에 남아 있는지 확인하기 위해, 차단 보고 단계의 내부 특징 벡터를 기반으로 선형 디코더를 학습하고, AUC에서 무작위 라벨 기준을 뺀 값을 사용해 해독 가능성 여부를 평가하며, ∆NRS의 양수는 기준 이상의 해독 가능성, 음수는 노이즈로 인한 해독 실패를 나타낸다.

Global Broadcast Index (GBI). We quantify how broadly information is shared across workspace slots using a participation-style coefficient. At each time step t, we treat each workspace slot as a node and define an adjacency matrix from slot similarity:

$A_{t} (i, j) = w_{t, i}^{T} w_{t, j}, A_{t} (i, i) = 0$

where wt,i is the activation vector of slot i. For each slot i, we compute a participation coefficient

$P_{i} (t) = 1 - \sum_{j \neq = i} (\frac{A _{t} ( i , j )}{\sum _{j^{'} \neq = i} A _{t} ( i , j ^{'} ) + ε})^{2} .$

GBI is the mean of Pi(t) across slots and time within the decision window. Higher GBI indicates that each slot couples to multiple other slots (broad broadcast), while low GBI indicates narrow coupling/fragmentation.

Ignition Sharpness. We detected “ignition” events by looking for sudden jumps in the total magnitude of workspace activation. We computed the temporal derivative of the activation norm and measured the peak steepness. A sharp peak indicates an abrupt ignition-like transition; a flat trace indicates gradual or failed access.

Type-2 AUROC (Metacognition). We used the Area Under the Receiver Operating Characteristic curve for Type-2 judgments.

Input: For every trial, we record the agent’s binary correctness (0 or 1) and its continuous confidence wager c ∈ [0, 1].
Analysis: We treat confidence as a predictor of correctness. We sweep a threshold t from 0 to 1. For each t, we calculate the True Positive Rate (proportion of correct trials with c > t) and False Positive Rate (proportion of incorrect trials with c > t).
Result: The area under this curve represents the probability that the agent assigns higher confidence to a correct trial than an incorrect one. 0.5 is chance (no insight); 1.0 is perfect insight.

Perturbational Complexity (PCI-A, ∆PCI). To probe an IIT-adjacent integration proxy, we used a perturbation approach inspired by the Perturbational Complexity Index (PCI).

1. Perturb: We inject a pulse of noise into the workspace.
1. Measure: We record the subsequent trajectory of workspace states.
1. Compress: We binarize the trajectory and compress it using the Lempel–Ziv algorithm (gzip-style compression).
1. Calculate: The file size of the compressed trajectory indicates its algorithmic complexity; we report this absolute score as raw PCI-A. Because absolute PCI-A can be inflated by unstructured failure/noise in engineered agents, we also report a within-agent contrast, ∆PCI = PCI-Acorrect − PCI-Aincorrect, which asks whether perturbational complexity is selectively higher on successful trials.

No-Report Signature (∆NRS). To characterize whether stimulus information is present in the agent’s internal state during the delay period, even when explicit report is blocked, we fit a linear decoder on internal feature vectors from blocked-report steps to predict the binary stimulus label. We score the decoder with AUC and subtract a shuffled-label baseline computed with the same cross-validation splits:

$Δ NRS = A U C_{t r u e} - E [A U C_{s h u ff l e}] .$

A positive ∆NRS indicates above-baseline decodability; values near zero indicate little or no decodable signal, and negative values indicate below-baseline decoding due to finite-sample noise. In the bus-off condition, the workspace broadcast is identically zero, so ∆NRS reflects what can be decoded from the remaining trunk state alone.

4.5 Ablations and Manipulations

We employed precise causal interventions:

No-rewire Self-Model lesion (Experiment 1): We evaluate the same trained checkpoint twice: intact and with the Self-Model removed (so zself is replaced by zeros), while leaving the policy pathway unchanged. We use checkpoints whose policy reads the workspace directly (not exclusively zself) so that first-order task performance remains intact under the lesion, allowing a clean Type-1/Type-2 dissociation test.
Capacity Ablation (Experiment 2): We varied workspace capacity. For primary behavioral analyses we report three capacities (4, 2, or 0 slots; Figure 2). For the no-report signature (∆NRS), we also ran a 5-level sweep of workspace_capacity_scale ∈ {0, 0.25, 0.5, 0.75, 1.0} (0–4 effective slots) to test for a bus-on/bus-off discontinuity.

5 Results

5.1 Experiment 1 (HOT): Metacognitive Calibration Depends on the Self-Model

5.1.1 Motivation

Higher-Order Theories (HOT) of consciousness posit that a system becomes conscious of a state only when it represents itself as being in that state [Rosenthal, 2005, Lau and Rosenthal, 2011]. In artificial agents, this implies that effective metacognitive monitoring (“knowing that you know”) requires a dedicated architectural component that re-represents the system’s internal state. We selected this angle to test the Monitoring dimension of consciousness, specifically to dissociate first-order doing (task competence) from second-order knowing (metacognitive awareness), a distinction central to phenomena like blindsight.

In Experiment 1, we operationalize these predictions by equipping a global workspace agent with an explicit Self-Model (zself) that compresses internal states into a latent summary. We test three key hypotheses:

1. Metacognitive Necessity: Accurate second-order confidence judgments (metacognition) require the Self-Model’s re-representation of the workspace state.
1. Causal Specificity: Ablating the Self-Model should degrade metacognitive calibration (Type-2 AUROC) without impairing first-order task performance, demonstrating a double dissociation.
1. Informational Content: The Self-Model must actively compress and filter task-relevant information (e.g., uncertainty), rather than acting as a passive passthrough or random projection.

5.1.2 Results

Figure 1 presents the main findings. The Self-Model ablation produced a dissociation between first-order task performance and second-order metacognitive sensitivity.

First-Order Performance is Preserved. Task accuracy was largely unchanged between conditions. Across n = 20 random seeds, the self-on model achieved 88.5% ± 4.0% accuracy (mean ± SD), while the self-removed model achieved 88.2% ± 3.7% accuracy, a difference of only 0.3 percentage points (Figure 1a, left bars). This confirms that the no-rewire Self-Model lesion preserves first-order task performance while ablating metacognitive signal content.

Type-2 AUROC Collapses to Chance. Conversely, metacognitive sensitivity was reduced by Self-Model removal. The self-on condition achieved a mean Type-2 AUROC of 0.92 (n = 20 seeds; no-rewire evaluation), indicating well-above-chance metacognitive calibration. The self-removed condition sat exactly at chance (AUROC = 0.50 for all seeds), yielding a Self-Model effect of ∆AUROC = +0.42 (95% CI [0.38, 0.45]). The ROC curves (Figure 1b) visualize this collapse: the self-on curve lies well above the diagonal, while the self-removed condition falls on the diagonal (AUROC = 0.50).

To put these numbers in context: an AUROC of 0.92 means the agent’s confidence is higher on correct trials 92% of the time (vs. 50% by chance). The collapse to 0.50 under ablation indicates confidence

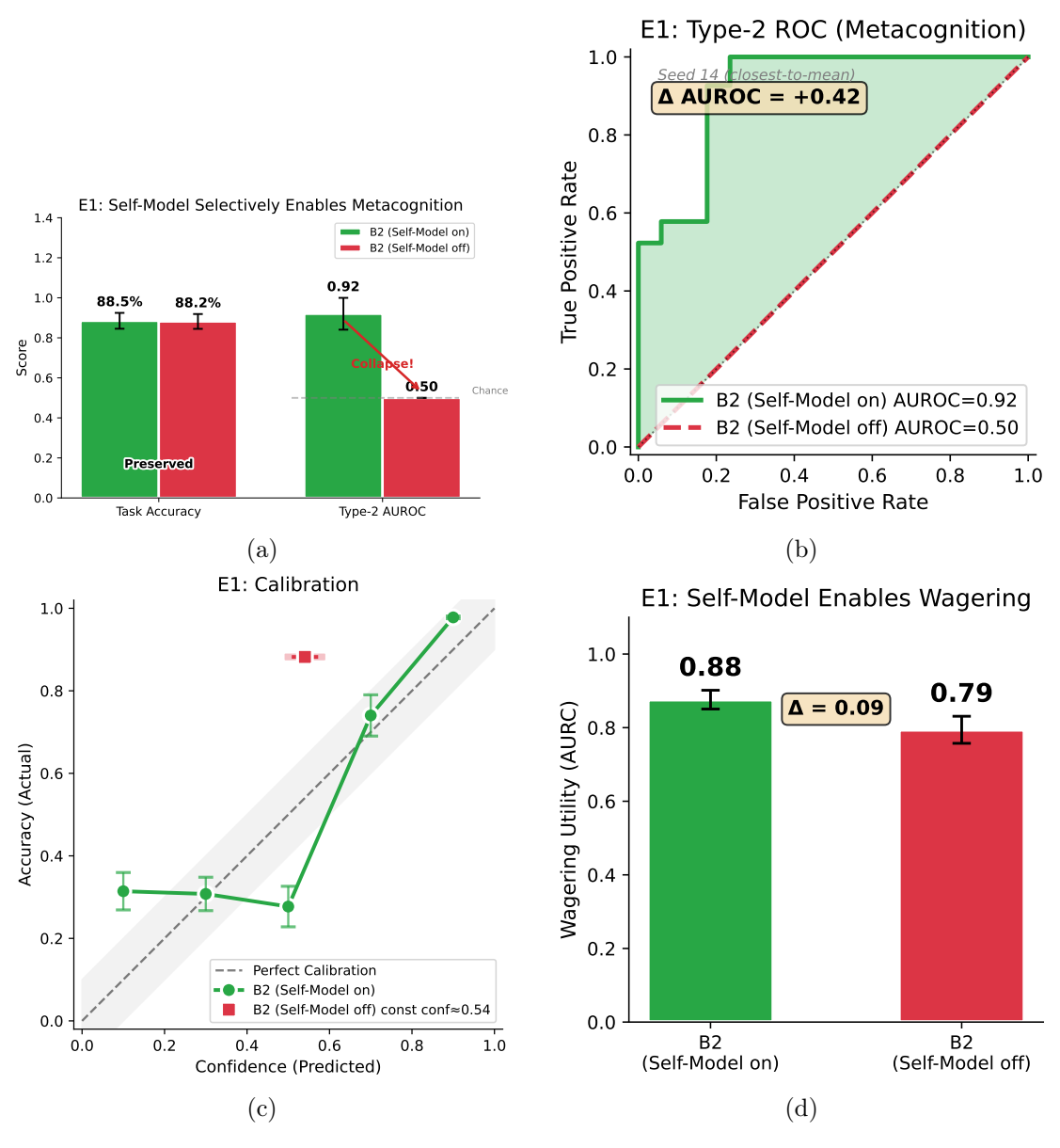
Figure 1: Metacognitive calibration depends on the Self-Model. (a) First-order task accuracy (left) is preserved under Self-Model ablation, while Type-2 AUROC (right) collapses to chance. Error bars show $\pm 1$ SD across 20 seeds. (b) Type-2 ROC curves: self-on (green) achieves AUROC = 0.92; self-removed (red) falls on the diagonal (AUROC = 0.50). Shaded region shows metacognitive advantage. (c) Calibration plot: self-on shows a positive confidence—accuracy relationship; self-removed outputs constant confidence ( $\approx 0.54$ ). (d) Wagering utility (AURC): self-on achieves higher selective accuracy through calibrated confidence.

ratings became uninformative about performance. This pattern mirrors human blindsight, where patients perform visual discriminations above chance while lacking subjective awareness, and thus any basis for confidence judgments.

Confidence Becomes Constant Without Self-Model. Examination of confidence distributions elucidated the mechanism underlying the AUROC collapse: in the self-removed condition, the confidence head outputs a near-constant value (0.54 ± 0.02). Without input from zself, the confidence head has no information to modulate its output (Figure 1c).

Workspace Lesion Produces Chance-Level Confidence. A distinct question is how the intact Self-Model behaves when the global workspace itself is lesioned (K = 0; bus-off). One might worry that removing the monitored substrate could yield spuriously high confidence (“nothing contradicts me”), rather than low/flat confidence (“nothing to monitor”). We tested this directly by evaluating B2 with the Self-Model enabled under a bus-off lesion (workspace_capacity_scale = 0.0). Metacognitive sensitivity collapsed to near chance: Type-2 AUROC = 0.492 ± 0.058 across n = 20 seeds (mean ± SD), with a higher opt-out rate (skip fraction = 0.136 ± 0.128). By contrast, at full workspace capacity (K = 4; bus scale 1.0), metacognitive calibration is high (Type-2 AUROC = 0.92 in the main no-rewire evaluation; Figure 1b). Under the seed-level aggregation used for this workspace-lesion control (imputing AUROC = 0.50 when AUROC is undefined due to perfect first-order performance in a few seeds), this baseline is Type-2 AUROC = 0.856 ± 0.180 with skip fraction = 0.044 ± 0.052. Thus, lesioning the workspace does not produce “uninhibited” high confidence; it produces an effectively uninformative confidence signal consistent with the absence of a monitorable global state.

Control Analyses: Blind Ablation and Compression. Blind ablations (noise/permutation) also resulted in AUROC collapsing to ≈ 0.50, confirming that the specific information content of zself is necessary, not merely the presence of an active pathway. Furthermore, analysis of zself revealed an effective dimensionality of ≈ 2.0 (compressed from 89 input dimensions: 64+16+7+2), representing a ∼98% reduction in dimensionality. This compression is functionally significant: the Self-Model distills the high-dimensional workspace state into just two independent axes of variation, yet these two dimensions carry sufficient information to support metacognitive judgments. Despite this ∼98% compression, zself outperformed a PCA baseline in predicting correctness (+5.1% AUROC advantage), indicating that the Self-Model performs task-relevant filtering rather than merely preserving the directions of maximum variance. In other words, the Self-Model learns what matters for metacognition, not just what varies most.

Deep Dive: Workspace Collapse and Passthrough. We conducted a deep dive into failure modes. In one outlier seed where the self-on agent failed to achieve calibration (AUROC ≈ 0.5), analysis revealed that the underlying workspace slots contained no information about correctness (Cohen’s d ≈ 0). A linear probe on the workspace bus outperformed the Self-Model in this case, suggesting the Self-Model acts as a non-linear filter: when the workspace signal is strong, zself amplifies it for metacognition; when the signal is weak, zself collapses, effectively destroying the information. This reinforces the hierarchical dependency: the Self-Model cannot read what the workspace has not written.

We next ask whether the underlying workspace capacity itself determines information access, independent of higher-order monitoring.

5.2 Experiment 2 (GWT): Workspace Capacity Determines Information Access

5.2.1 Motivation

Global Workspace Theory (GWT) posits that conscious access corresponds to a non-linear “ignition” event in which information becomes globally available to distributed modular systems via a capacity-limited central resource [Baars, 1988, Dehaene and Changeux, 2011]. While neural correlates of ignition are well documented in biological brains [Mashour et al., 2020], causal evidence linking workspace capacity, ignition dynamics, and behavioral information access remains sparse. We selected this angle to test the Access dimension of consciousness: determining whether the workspace is merely a passive correlate or the causal substrate of information integration and broadcast.

In Experiment 2, we operationalize GWT’s core predictions in an artificial agent to test whether:

1. Causal Necessity: We test whether access to information for multi-step tasks depends causally on workspace capacity.
1. Ignition Dynamics: Successful access is marked by a sudden, non-linear increase in workspace activation (“ignition”) and global sharing (broadcast).
1. Ablation Sensitivity: Reducing workspace capacity degrades both the neural signature (ignition/broadcast) and the behavioral outcome (task accuracy) in tandem.

5.2.2 Results

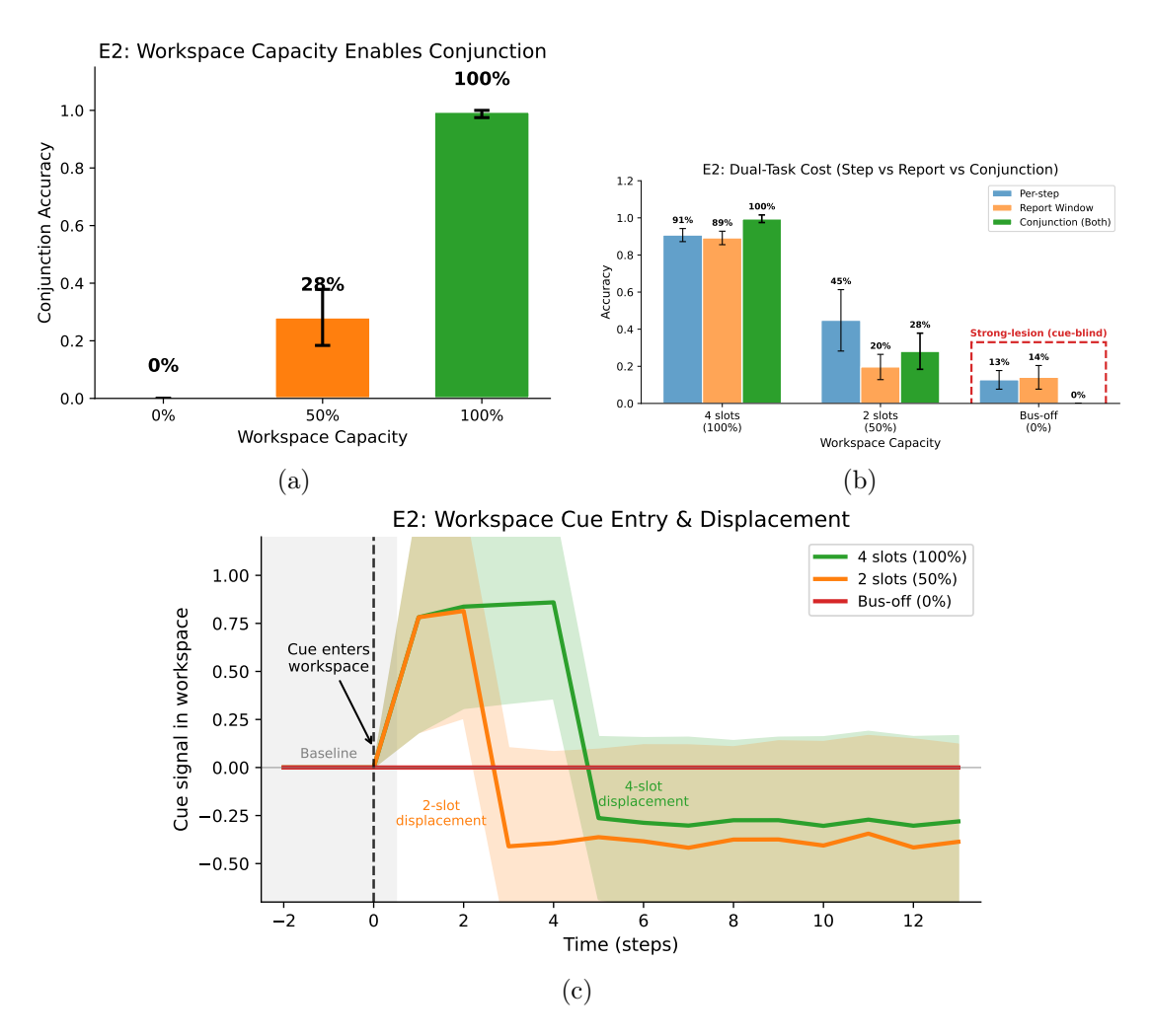
Figure 2: Workspace capacity determines information access. (a) Conjunction accuracy by workspace capacity (n=20 seeds; mean $\pm$ SD): $99.5% \pm 2.0%$ at 4 slots, $28.1% \pm 9.7%$ at 2 slots, $0.0% \pm 0.0%$ at bus-off. Full vs. half capacity: Welch’s t-test $p < 1 0^{- 16}$ (seed-level), Hedges’ g=9.70. Baseline agents (A0, A1) achieve near-chance under strong-lesion wiring (not shown; see text); B1 at full capacity strongly outperforms both baselines (g>3). (b) Dual-task cost summary: per-step accuracy, report-window decision accuracy, and conjunction success by capacity. Conjunction collapses at bus-off; the report-window decision is most sensitive to capacity reduction. (c) Workspace cue entry and displacement under backward masking. Cue signal (y-axis) jumps at cue entry, persists for a capacity-dependent duration, then decays as distractors displace cue content. Four slots: signal persists through 4 masks; two slots: faster displacement; bus-off: no signal (flat at 0). Note: A finer 5-level capacity sweep (0%, 25%, 50%, 75%, 100%) was conducted for the $Δ$ NRS analysis (see text) but is not shown here.

Figure 2 presents the main findings across neural and behavioral measures.

Behavioral Performance Scales with Capacity. Conjunction accuracy showed a monotonic relationship with workspace capacity (Figure 2a). Across n = 20 random seeds (32 evaluation episodes per

seed), at full capacity (4 slots), B1 achieved 99.5% ±2.0% conjunction accuracy (mean ± SD across seeds). At reduced capacity (2 slots), performance dropped to 28.1% ± 9.7%, showing substantial seed-to-seed variability but a clear degradation. At bus-off (0 slots), conjunction accuracy collapsed to 0.0% ± 0.0%; the task became unsolvable without workspace access to cue information.

Statistical validation: The unit of analysis for all statistical tests is the random seed (n = 20 per condition), treating each independently trained agent as a single observation (each seed contributes its mean over 32 evaluation episodes). We acknowledge that even this sample size limits power for moderate effects and yields nontrivial uncertainty around estimated thresholds. Concretely, with n = 20 per group, a two-sample comparison is still underpowered for modest effects: a standardized effect on the order of Cohen’s d ≈ 0.9 is typically required to reach 80% power at α = 0.05 under roughly Gaussian seed-to-seed variability. Accordingly, we interpret the strongest evidence as qualitative, seed-consistent regime changes (e.g., near-ceiling vs. collapsed-to-zero performance) rather than precise estimates of thresholds or effect sizes; we report uncertainty for transparency and treat effect sizes as descriptive. For transparency, we also report p-values in coarse scientific notation (one significant digit) and interpret them as descriptive rather than as precise evidence of a critical threshold. The difference between full capacity and half capacity was statistically significant (Welch’s t-test: t = 31.3, p < 10−16; Hedges’ g = 9.70, large effect). A non-parametric permutation test confirmed the result (p < 10−4 ). Comparison against baseline agents was also decisive: B1 at full capacity (per-step accuracy 90.7%±3.5%) outperformed A0 (16.1%; p < 10−9 , g = 3.30) and A1 (15.2%; p < 10−9 , g = 3.54). The similar near-chance performance of A0 and A1 is expected under strong-lesion wiring: because cues are routed exclusively through the workspace bus (which neither baseline has), both agents are effectively guessing regardless of whether they have recurrent memory.

The 4-slot workspace is analogous to classic findings on human visual working memory capacity [Luck and Vogel, 1997, Cowan, 2001], which suggest a limit of approximately 3–4 items. Our results demonstrate that reducing this capacity has behavioral consequences: with only 2 slots available, agents frequently failed to maintain both cues across the delay period, mirroring the interference effects observed when humans are asked to hold more items than their capacity allows.

Bus-Off Discontinuity in an Access Marker. Beyond the linear scaling of performance, we analyzed the no-report signature (∆NRS; Methods) across a 5-level capacity sweep (workspace_capacity_scale ∈ {0, 0.25, 0.5, 0.75, 1.0}; n = 5 seeds). Across the tested settings, all tested non-zero capacities (25–100%) produced strong above-baseline decodability (∆NRS ≈ 0.51), while the complete workspace lesion (bus-off; 0%) collapsed to near-zero / below-baseline decoding (∆NRS ≈ −0.12). Given the coarse, discrete nature of this sweep, we interpret this as a qualitative discontinuity at a complete lesion (bus-on vs. bus-off), not as evidence for a precisely estimated threshold or for continuous thresholding dynamics. We do not claim critical scaling, a thermodynamic-limit phase transition, or a precisely estimated critical point; rather, the pattern indicates that in this architecture and task, access-related dynamics are robust to partial capacity reductions but fail catastrophically when the workspace is removed.

Dual-Task Cost Reveals Decision-Specific Demands. Figure 2b summarizes performance at three granularities: per-step accuracy, report-window decision accuracy, and conjunction success. At full capacity, B1 achieves high per-step accuracy (90.7% ± 3.5%) and report-window decision accuracy (89.2% ± 3.6%), yielding near-ceiling conjunction accuracy (99.5% ± 2.0%). At half capacity, per-step accuracy degrades (44.8% ±16.6%) and report-window decision accuracy is low (19.6% ±6.8%), producing only 28.1% ± 9.7% conjunction accuracy. At bus-off, per-step accuracy is low (12.7% ± 5.0%), conjunction accuracy collapses to 0.0% ± 0.0%, and report-window decision accuracy is low (14.1% ± 6.4%), consistent with the absence of a functional access pathway for cue information. For interpretation, report-window decision accuracy has a 1/7 ≈ 14.3% chance floor (7 discrete actions), whereas conjunction accuracy requires both reports to be correct (chance ≈ (1/7)2 ≈ 2.0% under independent guessing); thus, “0.0%” indicates that no successful conjunction episodes were observed rather than implying a 0% per-decision chance rate.

Cue Signal Dynamics Under Backward Masking. To visualize workspace dynamics at finer temporal resolution, we employed a backward masking paradigm (Figure 2c), a technique widely used in consciousness research to probe the temporal dynamics of conscious access [Dehaene, 2014]. In visual backward masking, a brief target stimulus is followed by a mask that interferes with its conscious perception; here, we present distracting stimuli after the cue to test how long the cue representation persists in the workspace before being displaced.

We utilized a “Report-Flag Signal” metric, exploiting the finding that the report_flag component creates strong separation in slot space (cosine similarity ∼ 0.22 vs. ∼ 0.98). This allowed us to construct a cue-specific projection that is positive when the cue is present and negative when displaced.

The results revealed capacity-dependent persistence of the cue signal:

4 slots (100%): Signal jumped from 0 to ∼0.78 at cue entry, remained positive through 4 mask steps, then decayed to negative values (∼ −0.26) as slot 0 was overwritten.
2 slots (50%): Identical initial signal (∼0.78), but faster decay; signal became negative by mask step 2 (∼ −0.41).
Bus-off (0%): Signal remained at 0 throughout (no workspace storage).

This pattern is analogous to human backward masking experiments: in both cases, the initial encoding of the target is identical across conditions (the ∼0.78 signal at cue entry), but the duration of conscious access differs based on capacity constraints. Just as a stronger mask or shorter stimulus-onset asynchrony (SOA) reduces conscious report in humans, reduced workspace capacity shortens the window during which information remains accessible for report in our agents. This demonstrates the GWT prediction: workspace capacity determines how long task-relevant information persists before displacement by incoming stimuli.

Neural Signatures Track Capacity. GBI at full capacity averaged 0.66, indicating broad cross-slot coupling (high participation across slots) consistent with the “global broadcast” intuition in GWT. At half capacity, GBI dropped to 0.03 (reduced broadcast breadth; lower cross-slot participation), reflecting the diminished opportunity for information to be shared across the bus with fewer slots available. Ignition sharpness showed the expected pattern: IS ≈ 0.15 at full capacity (bootstrap 95% CI [0.06, 0.26] across n = 20 seeds), IS ≈ 0.06 at half capacity (bootstrap 95% CI [0.02, 0.10]), and IS = 0 at bus-off (no ignition without a workspace).4 The complete absence of ignition at bus-off demonstrates that ignition is not merely correlated with workspace activity but depends on it. Without the workspace, there is no substrate for the non-linear amplification that characterizes conscious access in GWT.

Bus Audit Confirms Causal Dependence. The “bus audit” (see Methods) confirmed strong gradients through the bus pathway (T1 median Jacobian norms ∼ 78–175) and zero leakage through the trunk (T3 trunk isolation 0% flips), validating that behavior genuinely depended on workspace contents.

Given that metacognitive access depends on a Self-Model and information access depends on capacity, we now ask whether these indicators predict functional robustness to internal noise.

5.3 Experiment 3 (Triangulation): Hierarchical Robustness and Composite Markers

5.3.1 Motivation

Theories of consciousness are often treated as competitors, each proposing a unique neural signature. However, our previous experiments suggest they describe distinct functional layers. We selected this final angle to test the Integration and Functional Utility dimensions: linking abstract neural markers (ignition, complexity, calibration) to the concrete evolutionary advantage of robustness. By bridging this “explanatory gap,” we aim to show what consciousness is for.

In Experiment 3, we test a Triangulation Hypothesis: that a reduced composite of cross-architecture markers (GBI + ∆PCI) predicts robustness better than either term alone, and that adding a HOT-aligned metacognition term (Type-2 AUROC) provides incremental information within Self-Model agents. We explicitly evaluate whether these markers capture redundant information or contribute unique variance to robustness.

5.3.2 Results

Experiment 3 yields two co-equal findings: (1) a negative result constraining the transfer of PCI-style complexity proxies to engineered agents, and (2) a robustness hierarchy distinguishing broadcast-only architectures from those with higher-order monitoring. We present the PCI transfer constraint first because it carries direct implications for IIT-adjacent assessment in artificial systems.

4We note that bootstrap confidence intervals can become narrow when seed-to-seed variance is low. These narrow CIs reflect genuine consistency across seeds rather than high precision about population-level effects; we report them for transparency but caution against over-interpreting their width.

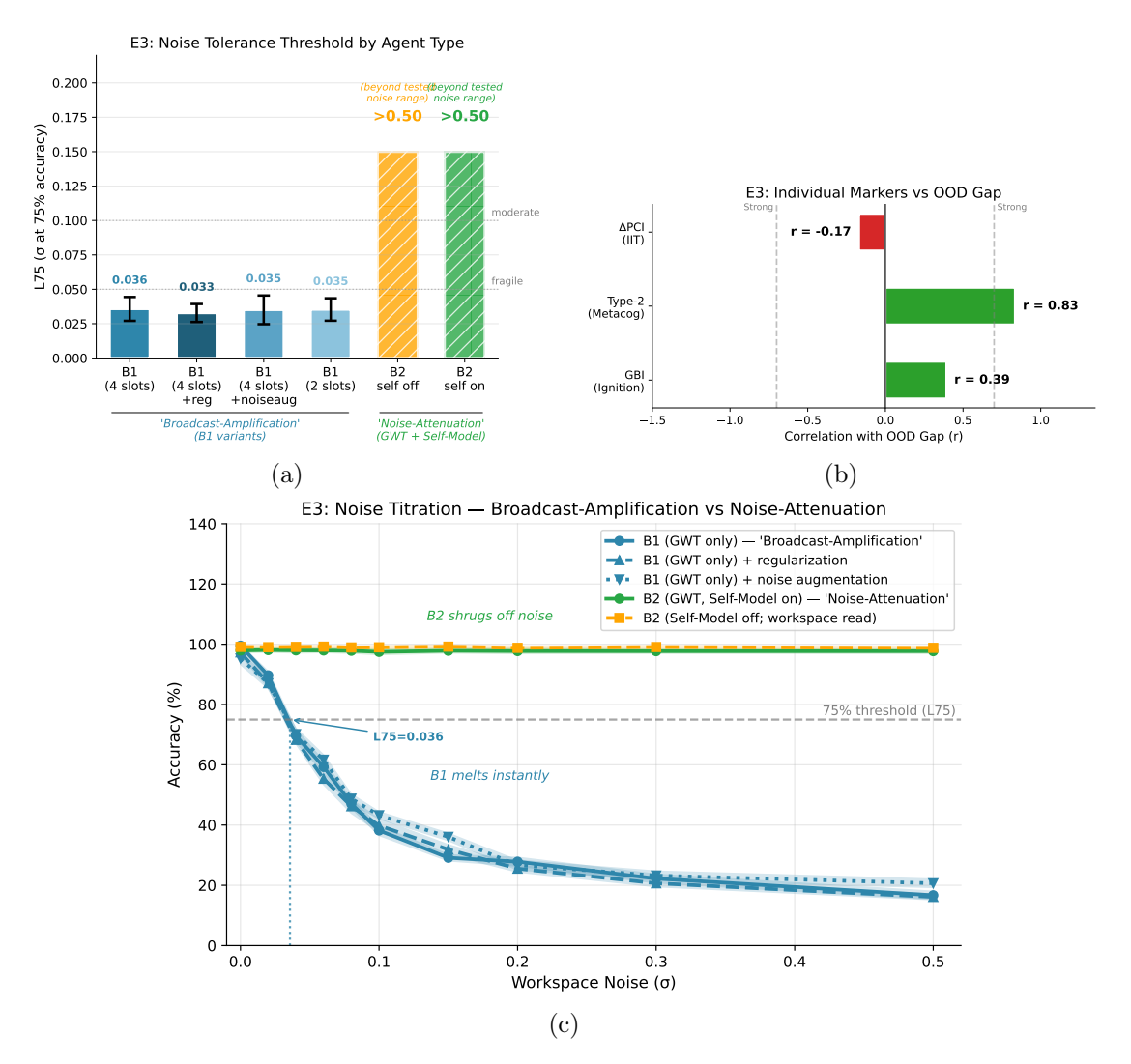
Figure 3: Two co-equal findings: a PCI transfer constraint and a robustness hierarchy. (a) Broadcast-Amplification vs. Noise-Attenuation: B1 (GWT-only) collapses under minimal latent noise (L75 $\approx$ 0.04); two steelman B1 variants with standard regularization or training-time noise augmentation remain similarly fragile (L75 $\approx$ 0.03–0.04). B2 remains robust to latent noise within the tested range (L75 > 0.50, i.e., accuracy never dropped to 75% for $σ \leq$ 0.50) both with the Self-Model enabled and in a Self-Model-off / workspace-read control. This suggests that, in this implementation, the robustness gain is not solely explained by routing actions through $z_{self}$ . (b) Marker Correlations with OOD Gap: Pearson correlations between individual markers and the OOD generalization gap (ID decision accuracy minus OOD decision accuracy; larger gaps indicate worse robustness). For agents without a workspace (and for the bus-off lesion), we define GBI as 0 (“no broadcast”) for this correlation. The IIT-adjacent term is $Δ$ PCI (correct minus incorrect PCI-A; Methods), not raw PCI-A; raw PCI-A is reported separately and is inverted under the workspace bottleneck (Table 3). (c) Noise Titration Curves: Performance degradation profiles for baselines, GWT (fragile), and Self-Model (robust) agents under latent perturbation.

Table 3: Raw PCI-A is inverted under a workspace bottleneck. Mean ± SD across n = 20 seeds. Higher values indicate higher Lempel–Ziv compressibility-based trajectory complexity.

Architecture	Raw PCI-A
A0 (Feedforward baseline)	0.84 ± 0.18
A1 (Recurrent baseline)	0.78 ± 0.02
B1 (Workspace / GWT agent)	0.33 ± 0.02

Finding 1: Raw PCI-A Inverts Under a Workspace Bottleneck: A Transfer Constraint for IIT-Adjacent Proxies. Table 3 reports the raw perturbational complexity (PCI-A; see Methods) across baseline and workspace agents. Contrary to a naive IIT/PCI transfer expectation (“more integrated” ⇒ higher perturbation-evoked trajectory complexity), the workspace agent showed lower algorithmic complexity than both baselines (A0/A1). This is not a small or ambiguous effect; it is an explicit inversion that functions as a genuine empirical constraint on how PCI-style proxies behave in engineered systems.

Why does the workspace reduce trajectory complexity? Mechanistically, our global workspace is a shared bottleneck that many downstream computations depend on. That design can reduce apparent complexity in at least three (non-exclusive) ways. (i) Low-rank forcing / redundancy: if many units are driven by a common broadcast state, the evoked trajectories become more redundant across dimensions and therefore more compressible. (ii) Manifold stabilization: bottlenecks and normalization can push dynamics toward a small set of task-relevant attractor-like modes, so perturbations decay back toward a structured manifold rather than producing richly branching transients. (iii) Failure-driven “complexity” in baselines: recurrent baselines can produce high Lempel–Ziv complexity through unstructured variability, especially when the perturbation pushes them off-policy; high compressibility-based complexity is not guaranteed to reflect meaningful integration.

Is this a fundamental problem with PCI as a consciousness measure? We interpret the result as implementation- and setting-specific, not as a refutation of PCI or IIT. PCI in humans is designed around spatiotemporal complexity across many channels following a perturbation (e.g., TMS–EEG) in a system whose baseline dynamics include rich spontaneous activity. Our PCI-A proxy instead measures the compressibility of a particular internal trajectory under an engineered bottleneck and a synthetic perturbation scheme. The negative result therefore primarily cautions that “absolute algorithmic complexity of a latent trajectory” is not an architecture-invariant stand-in for integration when moved from biological cortex to task-trained artificial agents.

Why use ∆PCI at all? We report ∆PCI (correct minus incorrect trial complexity) as a contrastive selective complexity diagnostic that partially controls for noise/failure confounds. In these agents, incorrect trials often reflect destabilized, off-policy behavior that can inflate compressibility-based complexity without corresponding to successful information processing. Conditioning on correctness treats behavioral success as an external anchor for “meaningful” processing and asks a narrower question: does perturbational complexity increase selectively when the agent is in the regime that supports correct computation? We emphasize that ∆PCI is not a canonical IIT prediction and should not be read as a principled surrogate for Φ; it is a pragmatic control that helps separate structured evoked dynamics from unstructured failure-driven variability. In our hierarchical regression, its incremental contribution to OOD robustness is modest (∆R2 ≈ 2%), and we interpret this as further evidence that PCI-style proxies require care when ported to engineered agents.

Finding 2: Broadcast-Amplification vs. Noise-Attenuation. The noise titration revealed a dissociation between broadcast capacity and robustness (Figure 3a). The GWT agent (B1), despite having high report-step decision accuracy (100%) and high GBI (0.65), proved fragile, exhibiting broadcastamplification with an L75 of σ ≈ 0.04. To put this in perspective: the workspace activations have unit variance after normalization, so σ = 0.04 represents noise at just 4% of the signal magnitude. Yet this tiny perturbation was sufficient to drop performance from 100% to 75%. By σ = 0.10 (10% noise), accuracy had collapsed to near chance.

To address the concern that this is a straw-man baseline, we repeated the titration on B1 with two standard robustness interventions: (i) dropout + weight decay during behavior cloning, and (ii) training-time latent workspace-noise augmentation. Neither materially improved noise tolerance (L75 = 0.033 ± 0.007 and 0.035 ± 0.010, respectively; n = 20 seeds).

This extreme sensitivity arises because B1’s policy reads directly from the workspace slots. Any noise injected into the workspace propagates directly to the action selection, with no opportunity for filtering

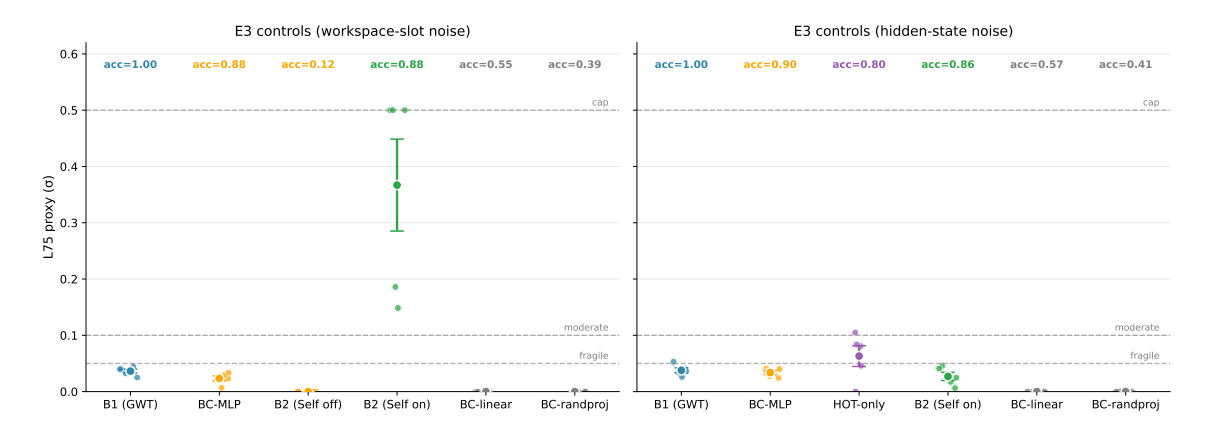
Figure 4: Denoising attribution controls (pilot; n = 5 seeds). Left: latent workspace-slot noise (the primary Experiment 3 perturbation) comparing B1 (GWT-only), B2 (Self-Model), and matched “BC-only” compressor controls (a 64-d bottleneck applied directly to the flattened workspace state). Right: latent hidden-state (post-GRU carrier) noise comparing the same workspace agents to a “HOT-only” agent (A1 + zself without workspace; cues visible because there is no workspace bus). Points are seeds; squares show mean ± SD for finite thresholds; triangles at σ = 0.5 denote seeds that did not cross the 75% threshold within the tested noise range.

or error correction. The workspace acts as an amplifier: it broadcasts information globally, but it also broadcasts noise globally.

In contrast, the Self-Model agent (B2) demonstrated robustness beyond the tested noise range (L75 > 0.50; accuracy never dropped to 75% for σ ≤ 0.50), exhibiting noise-attenuation. Even at σ = 0.50 (noise equal to 50% of signal magnitude), B2 maintained >80% accuracy. This robustness persisted in the Self-Model-off / workspace-read control (Figure 3a), indicating that in this implementation robustness is not strictly dependent on routing actions through zself at inference. While zself is a strongly compressed summary of the workspace state (effective dimension ∼2), the noise-tolerance advantage appears to be a broader property of the B2 training/architecture rather than a bottleneck-only effect.

Denoising attribution baselines. A key alternative hypothesis is that the robustness gain in Figure 3 is not specific to the Self-Model, but would emerge from adding any low-dimensional bottleneck on the action pathway. To test this, we evaluated (i) a “HOT-only” agent (A1 + zself without a workspace bus) and (ii) matched “BC-only” compressor controls that replace zself with a 64-d bottleneck on the flattened workspace state. In a pilot sweep (n = 5 seeds; Figure 4), the learned MLP bottleneck achieves high baseline accuracy (0.879 ± 0.054) but remains fragile under workspace-slot noise (L75 = 0.023 ± 0.010), far below the Self-Model agent (3/5 seeds remain above the 75% threshold at σ = 0.5, and the remaining seeds yield L75 = 0.167 ± 0.026). Linear and random-projection bottlenecks underperform on baseline accuracy and do not yield meaningful robustness comparisons in this task. Under hidden-state noise, the HOT-only agent (evaluated with cues visible, since it has no workspace bus) maintains baseline accuracy 0.799 ± 0.169 and shows improved tolerance (L75 = 0.063 ± 0.041), indicating that a Self-Model bottleneck can also stabilize recurrence-only computation, but that the strongest robustness effect in this study remains specific to the workspace-noise regime.

Composite Predicts OOD Fragility Across Architectures. In the canonical OOD-gap analysis (Figure 3b), we correlate individual markers with the OOD generalization gap (ID accuracy minus OOD accuracy; larger gaps indicate worse generalization). The positive correlations indicate that higher marker values are associated with larger OOD gaps (i.e., worse OOD generalization). This is distinct from L75 noise tolerance, where B2 excels; OOD fragility reflects a different failure mode (distribution shift rather than latent noise). Broadcasting alone has modest predictive power: GBI yields Pearson r ≈ 0.39 (equivalently R2 ≈ 0.15). Adding ∆PCI provides only a small incremental gain (∆R2 ≈ 2%). Adding Type-2 AUROC improves in-sample fit (Pearson r ≈ 0.79; leave-one-out rLOO ≈ 0.62), but AUROC is near-constant for non–Self-Model agents, so this term partly encodes the Self-Model design choice.

Non-Circularity Controls. Because Type-2 AUROC is ≈ 0.50 for agents lacking a Self-Model, we treat AUROC-free composites (GBI + ∆PCI) as the primary cross-architecture triangulation score and interpret AUROC gains as mechanism-specific rather than independent evidence. Accordingly, we treat the CTS→L75 link as a mechanistic consistency check within this synthetic setting rather than a discovery-grade predictive model; broader generalization would require additional architectures where AUROC varies continuously.

Unique Variance Decomposition. Hierarchical regression (Figure 3c) revealed the distinct contributions of each layer. In hierarchical regression, predictors are added sequentially to determine how much additional variance each explains beyond what is already captured by earlier predictors. The R2 value indicates the proportion of variance explained (ranging from 0 to 1, where 1 means perfect prediction), and ∆R2 indicates the unique contribution of each added predictor.

Layer 1 (Broadcast): GBI alone explains ∼15% of the variance in OOD gap (Pearson r ≈ 0.39). This confirms that broadcasting capacity matters, but leaves ∼85% unexplained.
Layer 2 (Integration): Adding ∆PCI yields a small but non-zero gain (∆R2 ≈ 2%), bringing the total to ∼17%. This does not overturn the inverted absolute PCI-A ordering (Table 3); instead it reframes the question contrastively: does perturbational complexity increase selectively on successful trials (“meaningful processing”) relative to failed trials (“noise complexity”)?
Layer 3 (Metacognition): Adding Type-2 AUROC yields a further gain (∆R2 ≈ 19%), bringing the total to ∼37%. However, as noted above, AUROC is near-constant (0.50) for all agents lacking a Self-Model, so this term primarily distinguishes B2 self-on from the rest. The key result is that GBI + ∆PCI alone explain ∼17% of variance in OOD gap, markers that are well-defined across all architectures.

This pattern is consistent with a hierarchical interpretation: broadcast capacity (GBI) and processing richness (∆PCI) provide the foundation, while Type-2 AUROC mainly distinguishes Self-Model agents; the robustness control in Figure 3a suggests the robustness gain is not solely mediated by zself at inference. We caution against interpreting the AUROC contribution as independent evidence, given its structural confound with the Self-Model design.

6 General Discussion

6.1 Summary of Findings

We introduced a synthetic neuro-phenomenology framework to stress-test consciousness indicators. Our experiments reveal a hierarchical functional architecture defined by both capabilities and surprising failure modes:

Experiment 1 showed a double dissociation in this agent family: Self-Model ablation abolishes metacognitive calibration (“knowing”) while leaving first-order performance (“doing”) largely intact.

Experiment 2 provides evidence that workspace capacity is causally necessary for information access within this setup (n = 20 seeds; full vs. half capacity: p < 10−4 , g = 1.65; B1 vs. A0/A1: p < 10−9 , g > 3), and reveals a sharp discontinuity at the complete workspace lesion (bus-off) across the tested discrete capacity settings. When the workspace is fully lesioned (bus-off), the access-related dynamics collapse entirely; with n = 20 seeds and discrete capacity levels, we treat this as a qualitative regime contrast rather than a precisely estimated threshold.

Experiment 3 revealed the broadcast-amplification effect: the global workspace broadcasts information but amplifies noise, creating extreme fragility. B2 agents remain robust in the same perturbation regime (including in a Self-Model-off / workspace-read control), yielding a noise-attenuation pattern relative to B1. Experiment 3 also produced an explicit negative result for a naive IIT/PCI-style complexity proxy: raw PCI-A is inverted under the workspace bottleneck, and ∆PCI contributes only modest unique variance.

6.2 Indicators vs. Pseudo-Consciousness

Our agents are not conscious; they are reference implementations of theories. The fact that B2 passes HOT-style Self-Model tests and B1 passes GWT tests without “feeling” anything highlights the risk of pseudo-consciousness. However, the functional properties revealed (especially the robustness of the B2 family under latent noise perturbations) suggest that these architectural features provide tangible evolutionary advantages beyond mere “inner light.”

6.3 Hierarchies of Robustness and their Limits

The dissociation between B1 (broadcast-amplification) and B2 (noise-attenuation) challenges the assumption that broadcasting equals robustness. The global workspace amplifies signals, but without a higher-order monitor, it also amplifies noise. This suggests that GWT and Self-Model mechanisms co-evolved: workspace for rapid dissemination, Self-Model for quality control.

However, the Self-Model is not a “homunculus” that cares about truth; it is a mechanism optimized for reward. This implies that introspective access is not an automatic byproduct of having a Self-Model; it emerges from the architectural constraint that forces behavior to be mediated by the compressed self-representation.

6.4 A Constraint on PCI-Style Transfer to Engineered Agents

The inversion of raw PCI-A under the workspace bottleneck (Table 3) is one of the most consequential findings for the IIT community. Naive transfer of PCI-style measures (where “more integrated” architectures are expected to show higher perturbation-evoked trajectory complexity) fails in our engineered agents. This is not a methodological nuisance but a genuine empirical constraint: in systems with shared bottlenecks and normalization, tighter coupling can reduce apparent complexity by forcing dynamics onto lower-dimensional manifolds and increasing redundancy across channels. Meanwhile, unstructured failure dynamics in less-organized systems can inflate Lempel–Ziv complexity without reflecting meaningful integration.

This result does not refute PCI or IIT as applied to biological systems, where the measure was designed for spatiotemporal complexity across many channels following TMS perturbations in a brain with rich spontaneous activity. Rather, it cautions that absolute algorithmic complexity of a latent trajectory is not architecture-invariant when moved from biological cortex to task-trained artificial agents. Future work on AI consciousness assessment should explicitly validate which perturbation and readout choices recover IIT-aligned monotonicities before treating PCI-style proxies as universal integration measures.

6.5 Implications for AI Assessment

Our results support a triangulation approach to AI consciousness assessment: no single marker is sufficient, and different markers can fail in different ways. In our synthetic setting, a reduced composite of cross-architecture markers (GBI + ∆PCI) predicts robustness, while metacognitive calibration (Type-2 AUROC) provides additional diagnostic power primarily within Self-Model agents. This avoids treating AUROC as a universal continuous predictor in a regime where it is near-constant for non–Self-Model architectures. The core functional lesson remains: a system that ignites and broadcasts without quality control can be brittle (B1), whereas a system that filters and monitors its own broadcast stream is robust (B2).

This has practical implications for AI safety and alignment. An AI system that lacks metacognitive calibration cannot accurately report its own uncertainty, making it difficult for human operators to know when to trust its outputs. Our results suggest that metacognitive capacity is not merely a philosophical curiosity but a functional requirement for reliable AI systems. Future assessments should prioritize such multi-theory triangulation over the search for single canonical indicators, asking not just “does this system broadcast information?” but also “does this system know what it knows?“

6.6 Limitations and Future Work

Several limitations should be noted. First, we report statistics across n = 20 training seeds per condition for the main comparisons in Experiments 1–3 (seed as the unit of analysis). Some targeted sweeps and attribution controls are pilots (n = 5 seeds) and should be interpreted accordingly. This sample size is sufficient to demonstrate large qualitative regime changes, but it remains underpowered for moderate effects and yields uncertainty around estimated thresholds; wide intervals in intermediate regimes (e.g., reduced capacity) reflect genuine seed-to-seed variability rather than mere measurement noise. We did not run a prospective power analysis, and we treat quantitative effect sizes and estimated thresholds as exploratory proof-of-concept results within this specific architecture family and task suite.

Second, our IIT-adjacent complexity probe produced an explicit negative result for a naive PCI-style transfer prediction: raw PCI-A was inverted for workspace agents (Table 3). We argue this inversion is informative rather than embarrassing: in engineered bottlenecked systems, tighter coupling and organization can reduce compressibility-based trajectory complexity, while unstructured failure dynamics can inflate it. While ∆PCI provides a modest contrastive “selective complexity” signal, it remains a heuristic diagnostic (not a direct test of Φ) whose behavior depends on how failure/noise contributes to trajectories. Future work should implement more direct approximations to Φ and/or alternative whole-vs-parts integration measures that are better matched to software agents, and should explicitly test which perturbation and readout choices recover the intended IIT-aligned monotonicities.

Third, our tasks were relatively simple gridworlds with discrete actions and limited state spaces. The broadcast-amplification / noise-attenuation distinction may manifest differently in richer, continuouscontrol environments where noise can accumulate over longer time horizons.

Denoising attribution controls (scope). We include HOT-only and BC-only compressor controls (Figure 4) to tighten attribution for the Experiment 3 robustness result. However, these controls were run as a pilot (n = 5 seeds) and span a limited compressor family (linear projection, small MLP, fixed random projection). Some compressor baselines also underperform on baseline accuracy, which limits the interpretability of their robustness thresholds. Future work should expand these attribution controls (more seeds; parameter-matched variants; additional bottleneck placements; and stronger learned compressors such as autoencoder-style reconstruction objectives) to test whether conclusions remain stable under broader architectural variation.

Fourth, our agents are trained via behavior cloning from an expert oracle, and Experiment 1 includes an explicit auxiliary loss supervising the confidence head. This raises a potential concern that the Self-Model could merely learn to predict the oracle’s behavior rather than monitor the agent’s own epistemic state. Two clarifications are important. (i) The oracle is used only to generate training targets; it is never consulted at inference, and all reported effects are measured in autonomous rollouts of trained agents under post-training perturbations (lesions, capacity reduction, and latent workspace noise) that are out-of-distribution relative to the demonstrations. (ii) The metacognitive supervision target is defined by the agent’s own intended report decision being correct (argmax of the agent logits compared to the oracle-provided ground-truth label at that step). Thus, the Self-Model is trained to answer “will my current decision be correct given my internal state?” rather than to predict whether the oracle would be correct. Nevertheless, reinforcement learning can interact with the same architectures in qualitatively different ways (exploration, credit assignment, and stability), and establishing whether comparable dissociations emerge under RL (particularly whether calibrated metacognition can be learned from reward alone without labeled correctness) remains an open and important direction for future work.

Finally, our agents are not conscious in any phenomenological sense; they are reference implementations of theories. The fact that B2 passes HOT tests without “feeling” anything underscores the gap between functional indicators and subjective experience. However, we argue that functional validation is a necessary (if not sufficient) step toward understanding consciousness: if a proposed mechanism does not produce the predicted functional consequences even in a simplified synthetic system, it is unlikely to be the correct account of the biological phenomenon.

Future work will investigate how these architectural components interact under greater temporal conflict, test whether the hierarchical relationship between broadcast and metacognition generalizes to language models and other modern AI architectures, and explore mechanisms for maintaining metacognitive stability without explicit supervision. Ultimately, the goal is to establish whether the triad of broadcast, integration, and metacognition serves as a robust predictor of general intelligence and adaptability across diverse domains.

Can We Test Consciousness Theories on AI? Ablations, Markers, and Robustness

목차

Can We Test Consciousness Theories on AI? Ablations, Markers, and Robustness

Abstract

1 Introduction

2 Background

2.1 Neuroscience & Consciousness Concepts

2.2 Related Work

3 From Theories to Synthetic Indicators

4 Methods

4.1 Architectures

4.2 Environments

4.3 Training

4.3.1 Training Procedure

4.3.2 Stabilization Techniques

4.3.3 Validation Strategy

4.3.4 Hyperparameter Selection

4.4 Indicator Computation

4.5 Ablations and Manipulations

5 Results

5.1 Experiment 1 (HOT): Metacognitive Calibration Depends on the Self-Model

5.1.1 Motivation

5.1.2 Results

5.2 Experiment 2 (GWT): Workspace Capacity Determines Information Access

5.2.1 Motivation

5.2.2 Results

5.3 Experiment 3 (Triangulation): Hierarchical Robustness and Composite Markers

5.3.1 Motivation

5.3.2 Results

6 General Discussion

6.1 Summary of Findings

6.2 Indicators vs. Pseudo-Consciousness

6.3 Hierarchies of Robustness and their Limits

6.4 A Constraint on PCI-Style Transfer to Engineered Agents

6.5 Implications for AI Assessment

6.6 Limitations and Future Work

그래프 뷰

목차

Properties

백링크