RR09. Backpropagation-3

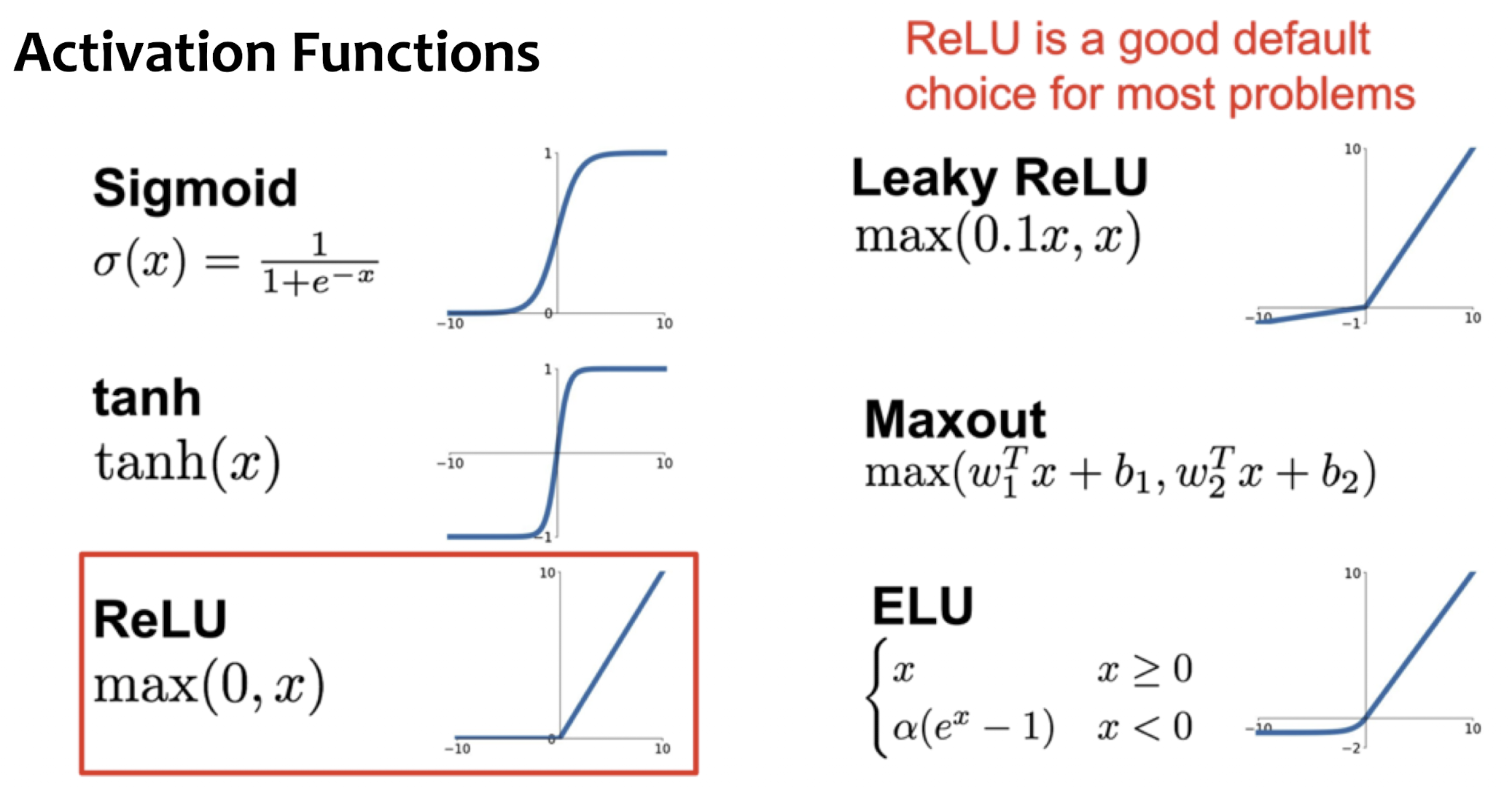
Activation Functions

---

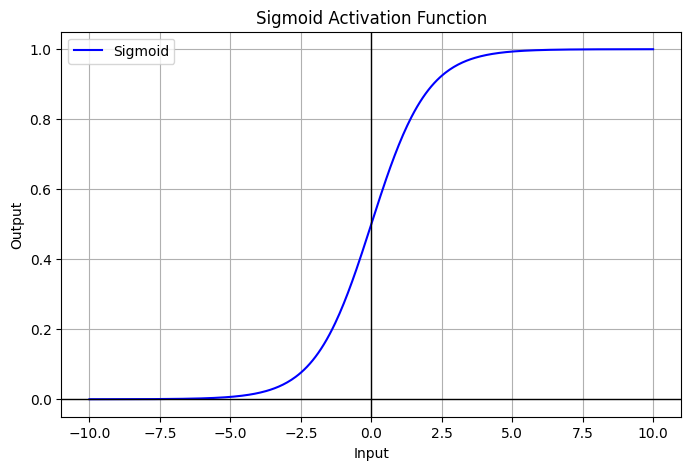
Sigmoid

Sigmoid

• activation 중 하나로 대표적으로 많이 사용됨.
  $g(x)=\frac{1}{1+\text{exp}(-x)}$
• range: $[0,1]$
• Neuroscience interpretation as saturating “firing rate” of neurons

Problems

• Saturation “kills” gradient : 입력 값의 절댓값이 커질수록 기울기 소실
  • 특히나 layer가 깊어질수록, chain-rule에 의해 곱해지는 term들이 많아질텐데, 그러면 앞 쪽에 있는 layer 들일수록 learning되지 않을 수 있지.
• Outputs are not zero-centered → introduces bias after the layer
  • sigmoid와 그 gradient는 항상 positive이기 때문에 model wight의 bias
  • $\mathrm{y}=g(\mathrm{ax}+\mathrm{b})$라 할 때, $\text{sgn}(\partial \mathcal{L}/\partial a_i)$ = $\text{sgn}(\partial \mathcal{L}/\partial g)$
  • 모든 gradient는 동일한 부호를 가짐.

다음과 같이 구현.

Sigmoid

def sigmoid(x: float) -> float:
	return 1 / (1 + np.exp(-x))

원본 링크

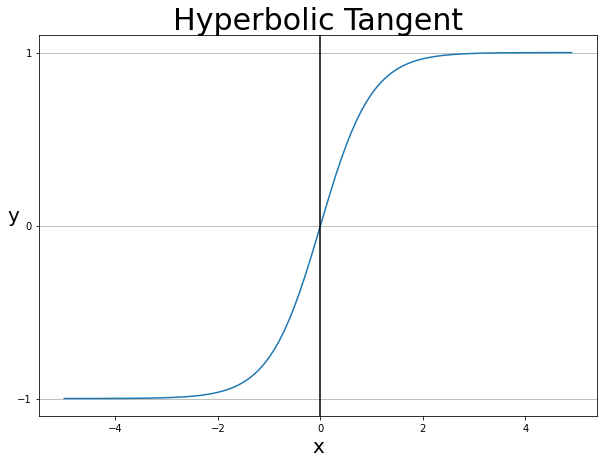
tanh

tanh(hyperbolic tangent)

• activation 중 하나로 대표적으로 많이 사용됨.
  $g(x)=\frac{2}{1+\text{exp}(-2x)}-1$
• range: $[-1,1]$
• anti-symmetric
• zero-centered

Problems

• Saturation “kills” gradient : 입력 값의 절댓값이 커질수록 기울기 소실
  • 특히나 layer가 깊어질수록, chain-rule에 의해 곱해지는 term들이 많아질텐데, 그러면 앞 쪽에 있는 layer 들일수록 learning되지 않을 수 있지.

다음과 같이 구현.

tanh

def tanh(x: float) -> float:
	return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

원본 링크

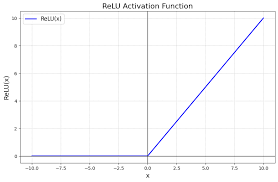
ReLU

ReLU(Rectified Linear Unit)

• activation 중 하나로 대표적으로 많이 사용됨.
  $g(x)=\text{max}(x,0)$
• Does not saturate(for $x>0$)
• Leads to fast convergence
• Computationally efficient

Problems

• No learning for $x<0$ → dead/dying ReLU
  • downstream gradient가 0(input이 0 이하일 때,)
  • often initialize with pos. bias ($b>0$)
• Outputs are not zero-centered → introduces bias after the layer
  • sigmoid와 그 gradient는 항상 positive이기 때문에 model wight의 bias
  • $\mathrm{y}=g(\mathrm{ax}+\mathrm{b})$라 할 때, $\text{sgn}(\partial \mathcal{L}/\partial a_i)$ = $\text{sgn}(\partial \mathcal{L}/\partial g)$
  • 모든 gradient는 동일한 부호를 가짐.

다음과 같이 구현.

ReLU

def relu(x: float) -> float:
	return np.maximum(0, x)

• 단점들 보안을 위해 Leaky ReLU 등이 있음.

How can we calculate non-differentiable function (like ReLU)?

→ Subgradient

원본 링크

Leaky ReLU

Leaky ReLU

• ReLU 보완형.
  $g(x)=\text{max}(x,0.01x)$
• Does not saturate(i.e., will not die)
• Closer to zero-centered outputs
• Leads to fast convergence
• Computationally efficient

Parametric ReLU

좀 더 generalized 된 버전이고, Leaky에서 0.01에 해당하는 것 조차 모델이 학습시킴.
$g(x)=\text{max}(x,\alpha x)$

• Does not saturate(i.e., will not die)
• Parameter $\alpha$ learned from data
• Leads to fast convergence
• Computationally efficient

원본 링크

ELU

ELU(Exponential Linear Units)

• Leaky ReLU 보완형.

x & \text{if } x > 0\\ \alpha (\text{exp}(x)-1) & \text{if } x \leq 0\\ \end{cases}$$ - All benefits of Leaky ReLU - Adds some robustness to noise - Default $\alpha = 1$

원본 링크

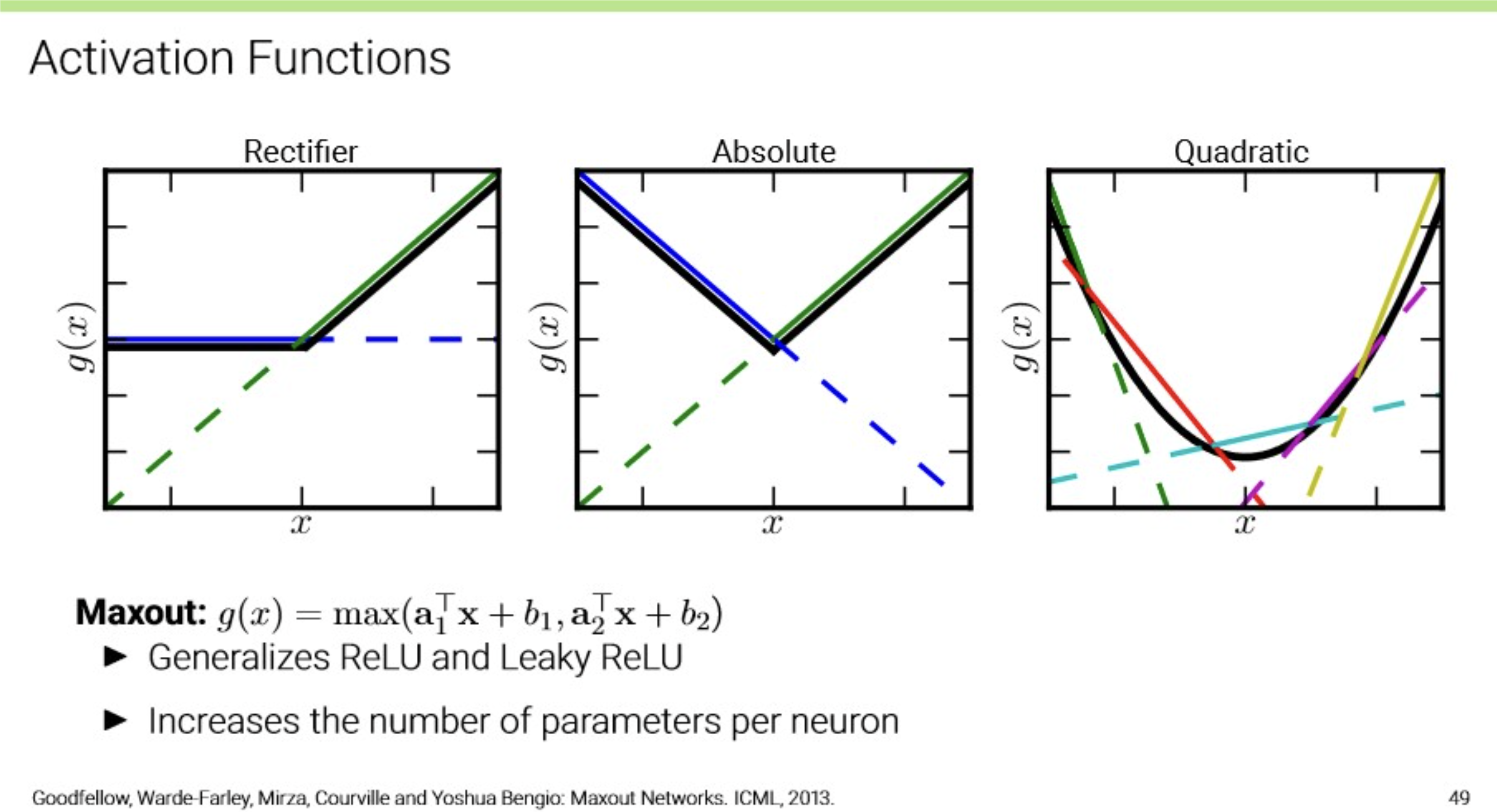
Maxout

Maxout

• Generalizes ReLU and Leaky ReLU
  $g(x)=\text{max}({\mathrm{a}}_1^{\top }\mathrm{x}+b_1,{\mathrm{a}}_2^{\top }\mathrm{x}+b_2)$
• Increases the number of parameters per neuron

원본 링크

Subgradient

---

Subgradient

원본 링크

Activation Functions

• 나중에 transformer 계열에 최근 가장 많이 사용되는 GeLU 계열이나 찾아볼 것.

Summary

• No one-size-fits-all: Choice of activation function depends on problem.
• We only showed the most common ones, there exist many more
• Best activation function / model is often using trial-and-error in practice
• It is important to ensure a good “gradient flow” during optimization

Rule of Thumb

• Use ReLU by default(with small enough lr)
• Try Leaky ReLU, Maxout, ELU for some small additional gain
• Prefer Tanh over sigmoid(Tanh often used in RNNs)

ReLU

ReLU(Rectified Linear Unit)

• activation 중 하나로 대표적으로 많이 사용됨.
  $g(x)=\text{max}(x,0)$
• Does not saturate(for $x>0$)
• Leads to fast convergence
• Computationally efficient

Problems

• No learning for $x<0$ → dead/dying ReLU
  • downstream gradient가 0(input이 0 이하일 때,)
  • often initialize with pos. bias ($b>0$)
• Outputs are not zero-centered → introduces bias after the layer
  • sigmoid와 그 gradient는 항상 positive이기 때문에 model wight의 bias
  • $\mathrm{y}=g(\mathrm{ax}+\mathrm{b})$라 할 때, $\text{sgn}(\partial \mathcal{L}/\partial a_i)$ = $\text{sgn}(\partial \mathcal{L}/\partial g)$
  • 모든 gradient는 동일한 부호를 가짐.

다음과 같이 구현.

ReLU

def relu(x: float) -> float:
	return np.maximum(0, x)

• 단점들 보안을 위해 Leaky ReLU 등이 있음.

How can we calculate non-differentiable function (like ReLU)?

→ Subgradient

원본 링크

Sigmoid

Sigmoid

• activation 중 하나로 대표적으로 많이 사용됨.
  $g(x)=\frac{1}{1+\text{exp}(-x)}$
• range: $[0,1]$
• Neuroscience interpretation as saturating “firing rate” of neurons

Problems

• Saturation “kills” gradient : 입력 값의 절댓값이 커질수록 기울기 소실
  • 특히나 layer가 깊어질수록, chain-rule에 의해 곱해지는 term들이 많아질텐데, 그러면 앞 쪽에 있는 layer 들일수록 learning되지 않을 수 있지.
• Outputs are not zero-centered → introduces bias after the layer
  • sigmoid와 그 gradient는 항상 positive이기 때문에 model wight의 bias
  • $\mathrm{y}=g(\mathrm{ax}+\mathrm{b})$라 할 때, $\text{sgn}(\partial \mathcal{L}/\partial a_i)$ = $\text{sgn}(\partial \mathcal{L}/\partial g)$
  • 모든 gradient는 동일한 부호를 가짐.

다음과 같이 구현.

Sigmoid

def sigmoid(x: float) -> float:
	return 1 / (1 + np.exp(-x))

원본 링크

tanh

tanh(hyperbolic tangent)

• activation 중 하나로 대표적으로 많이 사용됨.
  $g(x)=\frac{2}{1+\text{exp}(-2x)}-1$
• range: $[-1,1]$
• anti-symmetric
• zero-centered

Problems

• Saturation “kills” gradient : 입력 값의 절댓값이 커질수록 기울기 소실
  • 특히나 layer가 깊어질수록, chain-rule에 의해 곱해지는 term들이 많아질텐데, 그러면 앞 쪽에 있는 layer 들일수록 learning되지 않을 수 있지.

다음과 같이 구현.

tanh

def tanh(x: float) -> float:
	return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

원본 링크

원본 링크