Abstract
Abstract
Because of the “all-or-none” character of nervous activity, neural events and the relations among them can be treated by means of propositional logic. It is found that the behavior of every net can be described in these terms, with the addition of more complicated logical means for nets containing circles; and that for any logical expression satisfying certain conditions, one can find a net behaving in the fashion it describes. It is shown that many particular choices among possible neurophysiological assumptions are equivalent, in the sense that for every net behaving under one assumption, there exists another net which behaves under the other and gives the same results, although perhaps not in the same time. Various applications of the calculus are discussed.
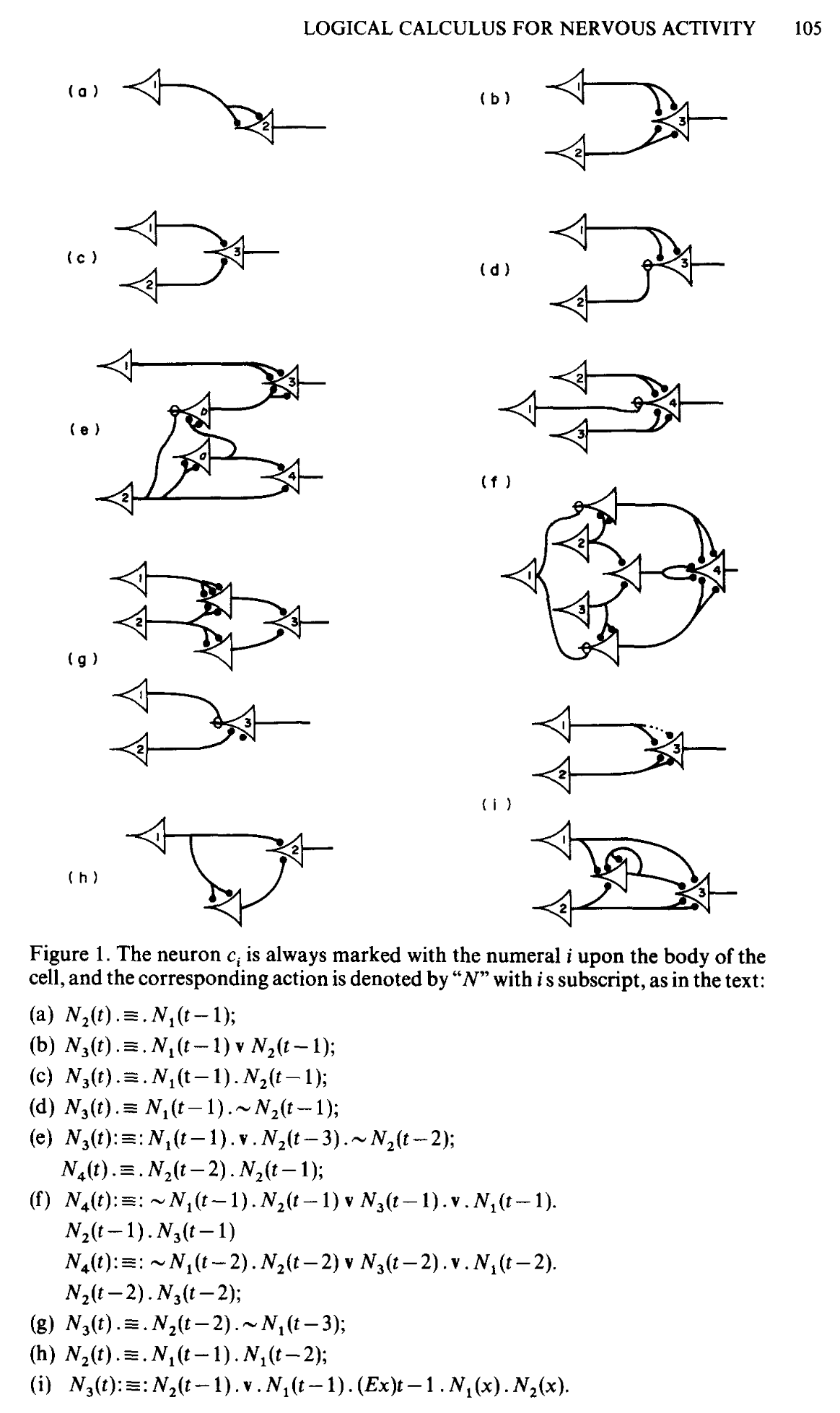
- 뉴런의 실무율(0 or 1) 특성을 논리 회로로 볼 수 있지 않을까? 에서 출발하여 이를 구조화 함.
- 다른 학문들(심리, 신경과학, 뇌 등)에서 다뤄지는 촉진, 억제 등의 활동이 근본적으로 equivalent 하다는 것을 주장.