Word2vec

NOTE

• Word2vec(Mikolov et al. 2013)에서 제안됨.
• Large Corpus로부터 학습시킴.
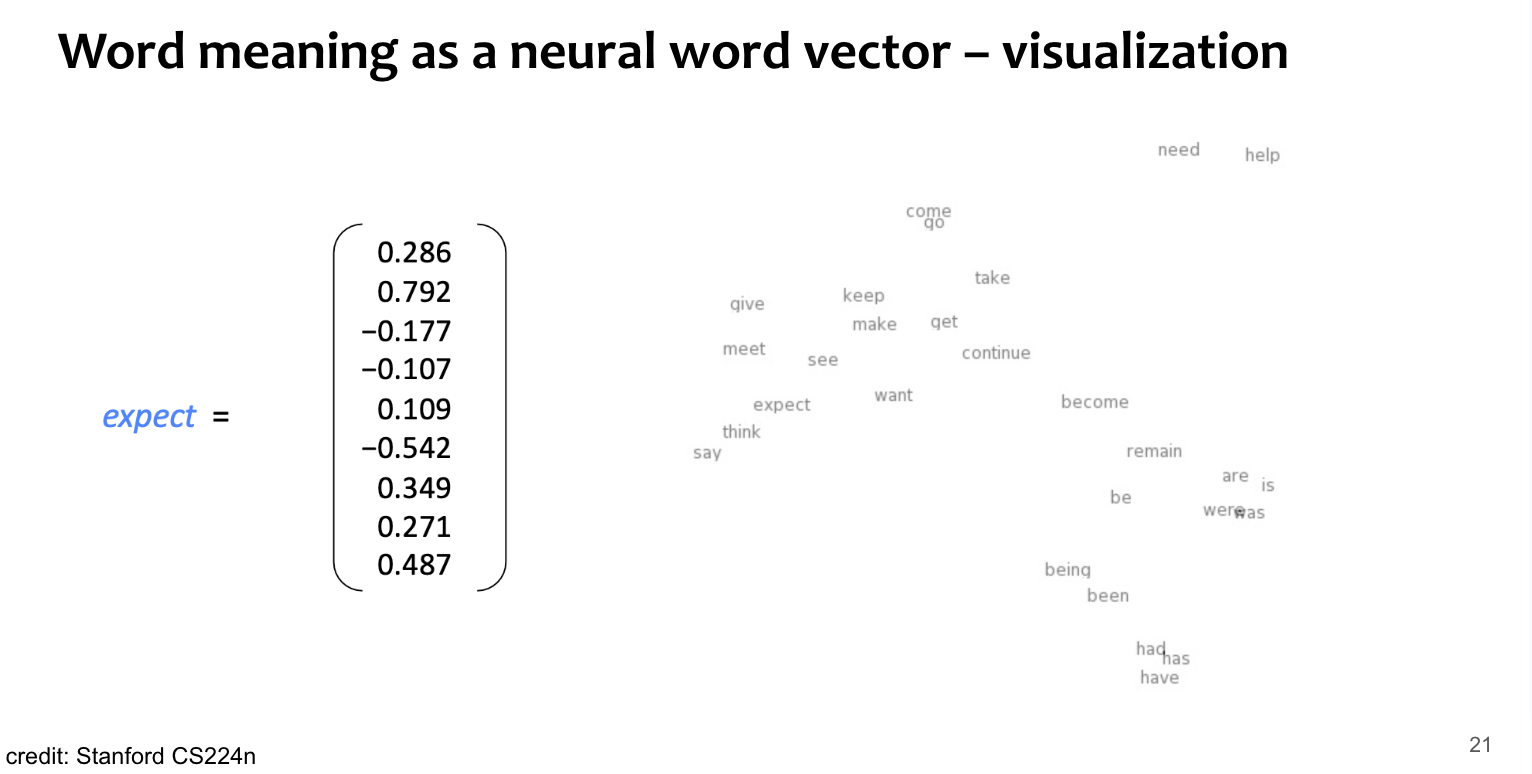
• 모든 단어들은 fixed 된 vector로 표현됨.
• notation:
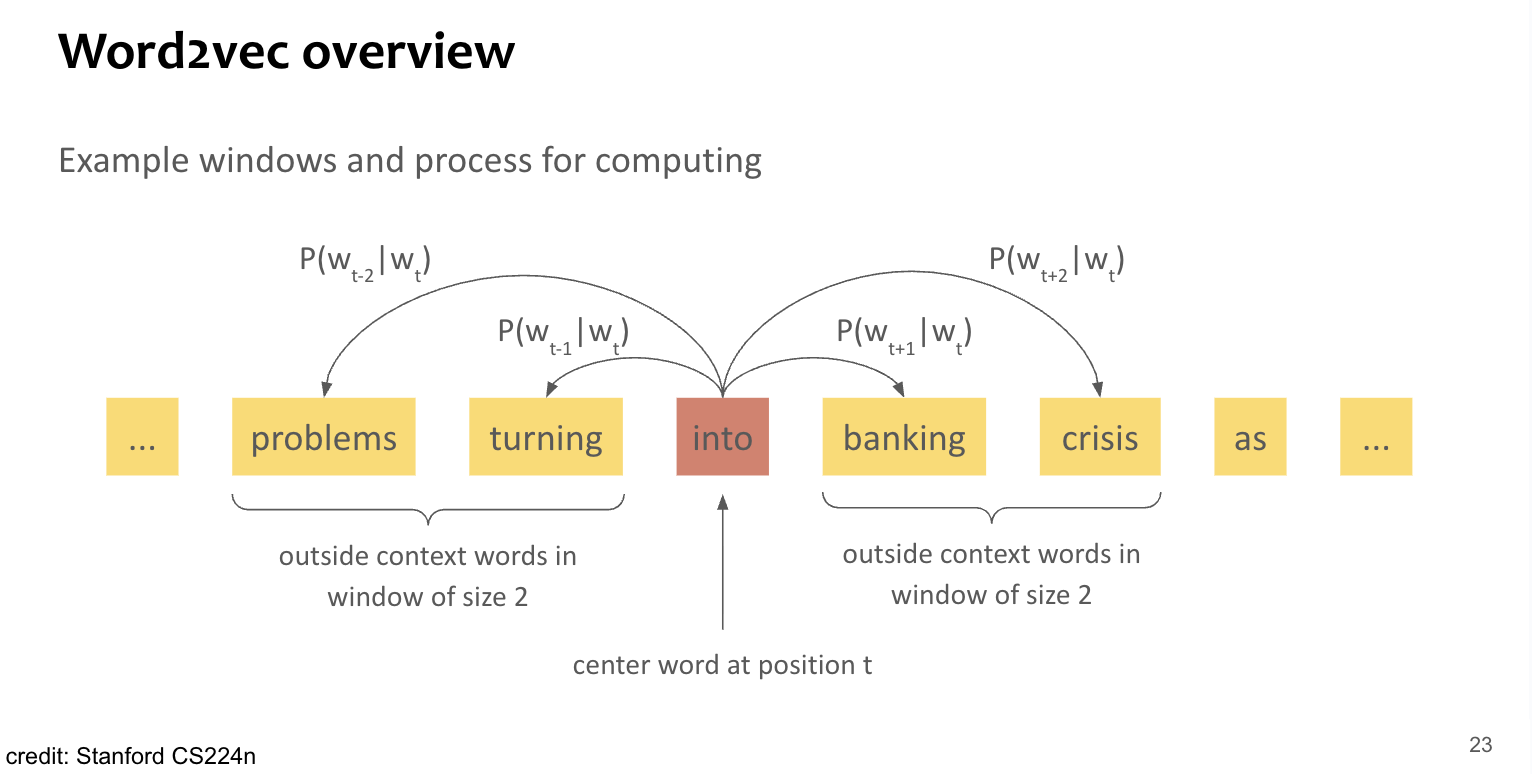
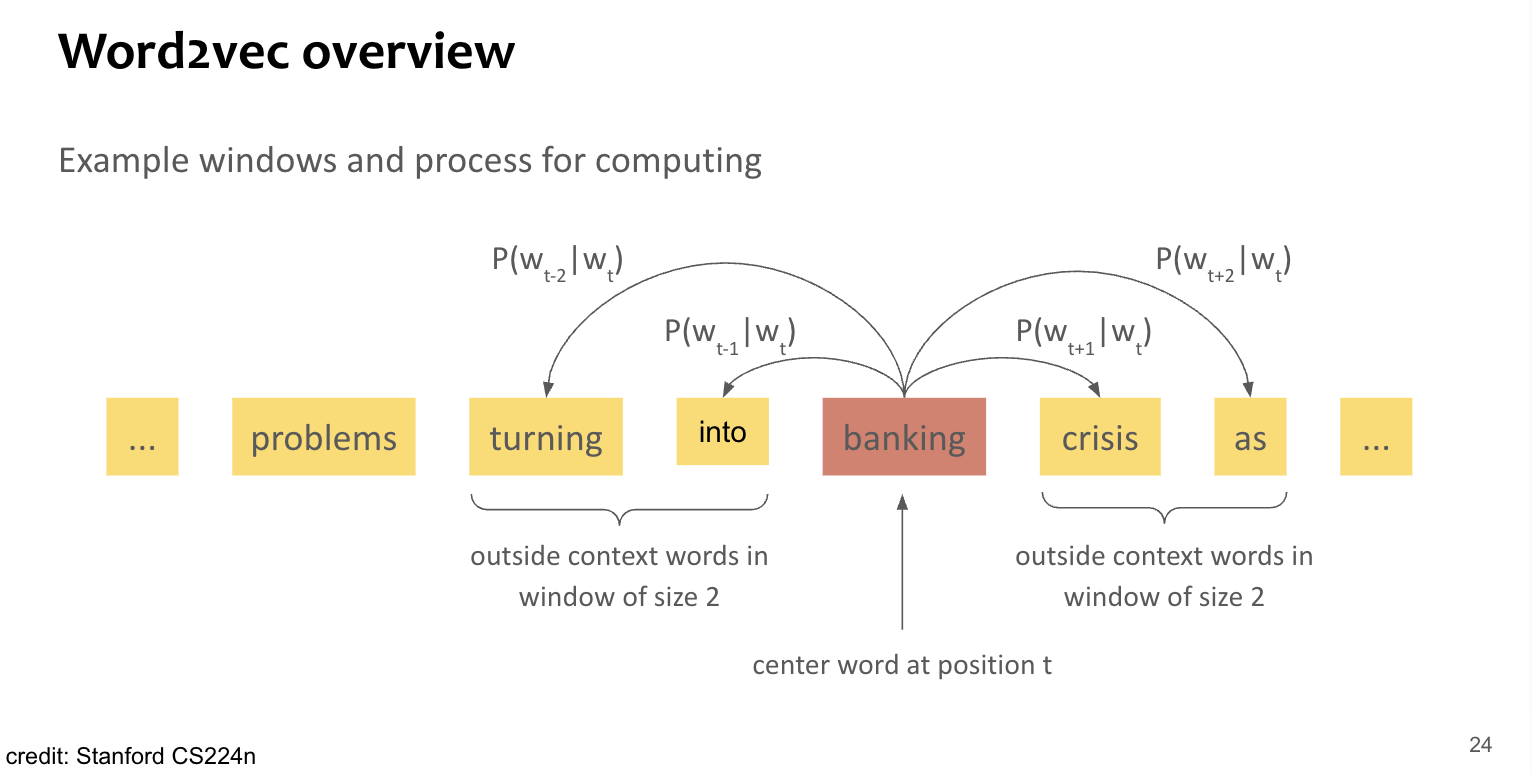
  • $c$ : center word
  • $o$ : outside word, i.e. context with fixed window-size
• 단어 벡터 간 유사도를 $c$와 $o$ 간의 conditional probability를 계산하는데 사용.
• 이 확률을 maximizing 하도록 word-vector 반복 수정.

Leaning

---

Overview

---

Example

Loss define

---

Summary

• 한 word에 대해서도 center로 사용될 때와 context로 사용될 때 다른 vector representation을 가진게 학습을 진행함.

$J(\theta )=\frac{1}{T}{\sum }_{t=1}^T{\sum }_{-m\le j\le m,j\ne 0}\text{log}p(w_{t+j}|w_t)$

$P(o|c)=\frac{\exp (u_o^T{v}_c)}{{\sum }_{w\in V}\exp (u_w^T{v}_c)}$

• Softmax와 비슷하게 생김.
• “max” : 큰 값들은 amplified하니
• “soft” : 작은 값들에도 여전히 확률 값을 주기는 하니까.

Training

---

Summary

Optimization target 즉, parameter는 모든 단어들의 vector embedding 자체. → voca size 만큼의 d-dimensional vector x 2(center version, context version)
즉,
$\theta \in {\mathbb{R}}^{2dV}$
where $d$: vector dimension, $V$: voca size

Question

Why 2 vectors?

• easy to optimize.
• average both at the end.

Summary

위 식을 통해 gradient를 계산해보면,
$\frac{\partial }{\partial v_c}\log \frac{\exp (u_o^T{v}_c)}{{\sum }_{w=1}^V\exp (u_w^T{v}_c)}$

Check

• 위에 건 v에 대한 미분. u에 대한 미분도 해볼 것.

Tip

Negative sampling이 training에 도움을 준다. (efficient vs naive softmax)

Model Variants(Type)

---

Skip-grams(SG)

---

• predict context by using center.
• course cover this .

Continuous Bag of Words(CBOW)

---

• predict center by using context.

Negative Sampling

---

Summary

위 식 중 확률 $P(o|c)$는 아래처럼 softmax항으로 생겼는데,
$P(o|c)=\frac{\exp (u_o^T{v}_c)}{{\sum }_{w\in V}\exp (u_w^T{v}_c)}$
denominator에서 sum term이 voca size라 연산량이 크다.

따라서 naive하게 softmax를 사용하지 않고, negative sampling을 사용한다.

Important

Main Idea: train binary logistic regression for a true pair(center word and a word in its context window) vs several “noise” pairs (the center word paired with a random word)

Quote

From “Distributed Representations of Words and Phrases and their Compositionality” (Mikolov et al. 2013)

$J_{neg-sample}(u_o,v_c,U)=-\log \sigma (u_o^T{v}_c)-{\sum }_{k\in \{Ksampledindicies\}}\log \sigma (-u_k^T{v}_c)$

• k개의 negative samples(using word occurance probabilities)
• Aim: 실제 context 내부에서 발견되는 단어들의 확률은 maximize, 반대로 negative sample 항들에 대한 확률은 minimize.

Tip

$U$가 negative sample 추출 시 사용되는 확률 분포이자, occurance distribution인데, 이를 그대로 사용하는 것보다 $U^{3/4}$해서 사용하는 것이 경험적으로 더 좋다고 한다.

• 3/4 power 걸어주면, 저 빈도 단어들이 조금 더 추출되는 효과.

SG(stochastic gradient) with neg sampling

---

NOTE

업데이트 대상인 vector representation들은 voca size만큼 있으니, 이 한 번의 업데이트 시 현재 주목하는 단어들만 update하면 되는 거지, 나머지 단어들은 건드릴 필요가 없음. → stochastic process를 해야 함.

We might only update the word vectors that “actually appear”!

Solution:

1. either you need sparse matrix update operations to only update certain rows of full embedding matrices U and V,
2. or you need to keep around a hash for word vectors

If you have millions of word vectors and do distributed computing, it is important to not have to send gigantic updates around!